Why Did Sumerians Use the Sexagesimal System?
Sumerians used sexagesimal numerals not only because the number 60 has many divisors or it is countable on the fingers of both hands but because 60 is the least common multiple of the number of fingers of both hands and the number of months in a year. The Chinese cycle of the Stems and Branches has the same structure as the Sumerian sexagesimal system and we can assume the Chinese sexagesimal cycle was imported from Mesopotamia to China. Today both the Mesopotamian sexagesimal system and the Chinese sexagenary cycle are apt to be explained in terms of the 60-year conjunction cycle of Jupiter and Saturn, such an interpretation of posterity should not conceal the original implication.

Contents
1. What structure did the Mesopotamian sexagesimal system have?
First we will survey the Mesopotamian numerals and units of measurement and recognize what structure the Mesopotamian sexagesimal system had and what relation it had to their units of measurement.
1.1. The Mesopotamian numeral system
Sexagesimal is a numbering system whose base is sixty. It originated in the ancient Sumerians in the 3rd millennium BC and was passed down to the ancient Babylonians and other nations. It is still partially used for measuring time and angles. The numeral system we now usually use is the decimal (10-base) system and the number 123 is equivalent to 1×102+2×101+3×100, while 1 hour, 2 minutes and 3 seconds is equivalent to 1×602+2×601+3×600=3723 (seconds).
Sexagesimal is uncommon as a general counting system. We can find an exceptional use among the Ekagi people of Western New Guinea[1]. The Egyptian, the Greek and many other nations adopted the decimal system. No counting method is as natural as that of turning in each finger and since we have 10 fingers the decimal system is the most common.
The reason Maya numerals were vigesimal (20-base) is also anatomical. We have 10 fingers and 10 toes. Each limb (hand or foot) can count up to five and this is why many decimal or vigesimal systems include quinary (5-base) subsystem. The figure below shows the sub-base of Maya’s vigesimal system is five, where one dot seems to represent one finger/toe and one horizon one limb.
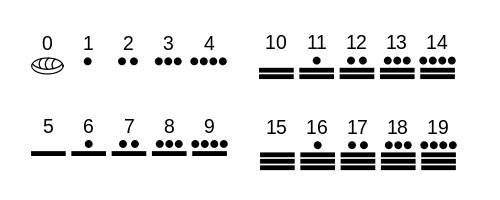
The Sumerian sexagesimal system used ten as a sub-base. The following table indicates that the vertical wedge (V) represents 1 and the horizontal one (<) 10. It is decimal until it reaches 59. The Sumerian used a decimal system around 3500 BC and then their system evolved into the sexagesimal.

As their system lacked zero, 1 and 60 were not distinguishable from their appearance. Distinguishing them from their context was inconvenient and so a sign for blank space was later invented.
1.2. The Mesopotamian units of measurement
A nation’s system of measurement does not necessarily reflect their system of numerical notation. Britain, for example, had used the anomalous system of currency unit until February 1971: 1 pound = 20 shilling, 1 shilling = 12 pence, although their numerals are decimal. The Mesopotamian system was not less anomalous than the British. Let us survey their system and its relation to the sexagesimal numerals.
The following table shows the ancient Mesopotamian units of length. The unit order of 60 must have been too large without introducing intermediate units. Since the ratio of units is either a divisor or a multiple of 60, the sexagesimal can simplify the notation of length.
| Unit | Ratio | Ideal Value | Sumerian | Akkadian |
|---|---|---|---|---|
| grain | 1 | 1/360m | še | uţţatu |
| finger | 6 | 1/60m | šu-si | ubānu |
| foot | 2×60 | 1/3m | šu-du3-a | šīzu |
| cubit | 3×60 | 1/2m | kuš3 | ammatu |
| step | 6×60 | 1m | ĝiri3 | šēpu |
| reed | 18×60 | 3m | gi | qanû |
| rod | 36×60 | 6m | nindan | nindanu |
| cord | 6×602 | 60m | eše2 | aslu |
The next table shows the ancient Mesopotamian units of area. Their standard is 1 sar = 1 nindan which is a unit of field with 10 seeding lines.
| Unit | Ratio | Dimensions | Ideal Value | Sumerian | Akkdian |
|---|---|---|---|---|---|
| garden | 1 | 1 nindan × 1 nindan | 36m² | sar | mūšaru |
| field | 100 | 10 nindan × 10 nindan | 3,600m² | iku | ikû |
| estate | 1,800 | 30 nindan × 60 nindan | 64,800m² | bur | būru |
The form of bur is not a square, because their farm is long along the seeding lines. The relation of sar to iku is decimal, but that to bur is partially sexagesimal.
The next table shows the ancient Mesopotamian units of volume. The cube of 6 šu-si is defined as 1 sila3.
| Unit | Ratio | Ideal Value | Sumerian | Akkdian |
|---|---|---|---|---|
| shekel | 1 | 1/60L | gin2 | šiqlu |
| bowl | 60 | 1L | sila3 | qû |
| vessel | 10×60 | 10L | ban2 | sutū |
| bushel | 602 | 60L | ba-ri2-ga | parsiktu |
| coomb | 5×602 | 300L | gur | kurru |
These units were used to measure the volume of barley seeds. 1 gin2 seeds were necessary to sow along 1 nindan long line, 1 sila3 seeds were necessary to sow along 60 nindan long line and 1 gur seeds were necessary to sow in 60 nindan long and 1 bur wide field[4]. The units of area were related to those of the volume of seeds in this way.
The next table shows the ancient Mesopotamian units of time. One year is divided into 12×30 = 360 days and one day is divided into 12×30 = 360 sub-units. Ironically the base of Sumerian time notation was not 60 but 360, although the base of our time notation is 60.
| Unit | Ratio | Ideal Value | Sumerian | Akkdian |
|---|---|---|---|---|
| gesh | 1/360 | 240s | mu-eš | geš |
| watch | 1/12 | 7,200s | da-na | bêru |
| day | 1 | 86,400s | ud | immu |
| month | 30 | 2,592,000s | itud | arhu |
| year | 360 | 31,104,000s | mu | šattu |
The Sumerians had 12 hours in a day, but at some point this was changed to 24 hours.
2. Why was the number 60 valued in Mesopotamia?
Many scholars have proposed hypotheses as to the reason Mesopotamia adopted sexagesimal without reaching consensus. Here we examine the representative hypotheses.
2.1. 60 is a highly composite number
The most popular hypothesis proposed since Theon of Alexandria (Θέων; ca. 335 – ca. 405) is that Sumerians valued 60 because it has many divisors. To be sure it has 12 divisors, namely 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 and it is easy to reduce a fraction with 60 its denominator. The figure below tells that no positive integers less than 120 have more divisors than 60.
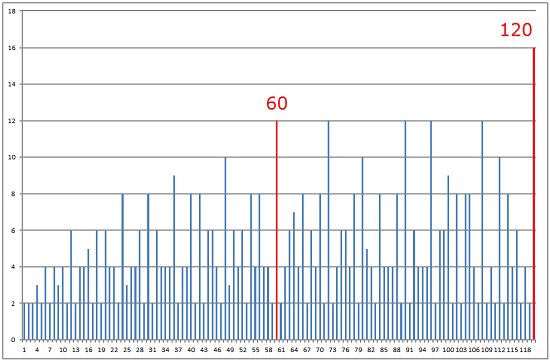
A positive integer with more divisors than any smaller positive integer like 60 is called a highly composite number (HCN). HCN goes for a unit of measurement because of its divisibility. For example, the numbers of 12, a dozen, and 360, the degrees in one full rotation, are HCNs. As we have already recognized, the ratio between Mesopotamian units of measurement is either a divisor or a multiple of 60. It follows Sumerians did not use 7 as the base of their numerals because it is not a HCN, although they regarded 7 as a sacred number.
On the other hand the most widely used base, 10, is not a HCN and a relatively small HCN, 48, is never used as a base. So, being a HCN is neither necessary nor sufficient condition to be a base. It is just one of the reasons that 60 became the base of Mesopotamian numerals.
Some insist that 60 is the unique number with the most consecutive factors under the breakpoint of factors[5]. That is to say, the breakpoint of 60 is
and when you divide 60 into a pair of its divisors,
60=1×60, 2×30, 3×20, 4×15, 5×12, 6×10
you can find that the divisors less than the breakpoint (1, 2, 3, 4, 5, 6) are consecutive. When you divide 12 into a pair of its divisors,
12=1×12, 2×6, 3×4
you can find that the divisors less than the breakpoint (1, 2, 3) are also consecutive, but no other positive integer has more consecutive factors under the breakpoint than 60. Does this mathematical fact have any significance? It might be convenient when you list all divisors of such numbers, but there are no other merits. Taking it into consideration that Sumerians attached importance to 12, I think the mathematical fact that 12 is not only a divisor of 60, but also the number of the divisors of 60 is more important.
2.2. 60 is countable on the fingers of both hands
The decimal system is most widely used because you can count 10 on the fingers of both hands. Can’t we justify the Mesopotamian sexagesimal system by the same fact?
On the subject of a measurement system based on twelve, Georges Ifrah seems more persuasive. He argues that the twelve-part numbering system, like the related sixty-part numbering system, goes back to a long-established and widely used finger-counting method. As he puts it, the “duodecimal finger-counting method used in India, Indo-china, Pakistan, Afghanistan, Iran, Turkey, Iraq, Syria and Egypt" involves counting to twelve. One does this by using the thumb of the right hand, beginning with the outermost of the three bones at the tip of the little finger. The sexagesimal finger-counting method, still used in most of the same countries, is complementary to the duodecimal one. It uses the left hand to indicate twelve, twenty-four, thirty-six, forty-eight, and sixty by closing down each of the five fingers, starting with the little finger and finishing with the thumb. [6]
If this finger-counting method was the reason for the Mesopotamian sexagesimal system, why was its sub-base 10 instead of 12? It is inconsistent that the counting system is 12×5=60, while the notation system is 10×6=60. Note that Egypt uses this duodecimal finger-counting method. The Ancient Egyptians had a decimal system and did not accept a sexagesimal system. They did not need to count 60, but they divided day and night into 12 hours each and they needed to count 12. Therefore we can safely assume that this finger-counting method was originally developed to count 12 and later converted to count 60 and that Sumerians developed the sexagesimal notation independent of this counting method.
The biggest number you can count in this way is not 60. Use the left hand to count 12 as well, and you can count up to 122=144, that is to say, duodecimal two-digit figures. If counting the biggest number on the fingers of both hands is important, the duodecimal system should be adopted and if easy counting on the fingers of both hands is important, the decimal system should be adopted. Why did Sumerians invent the intermediate sexagesimal system that was good for neither one purpose nor the other?
2.3. 60 has an astronomical significance
A clue to answering why Sumerians had the sexagesimal system while Egyptians had the decimal lies in the difference between their calendars. Egyptians used the solar calendar, while Sumerians used the lunisolar calendar. The lunisolar calendar is a calendar based on both lunar and solar cycles. As the moon phase changes every 30 days (more exactly 29.53), 30 or 29 days must be 1 month. Then 12 months is shorter than the 365-day tropical year. So, every second or third year has 13 months to adjust the gap. The Egyptian solar calendar defined 365 days as 1 year and their month did not reflect the moon phase cycle. So, we can say Egyptians were interested in solar cycles and Sumerians paid close attention to lunar cycles as well.
This difference in interest seems to have resulted from their difference of their location. The major city-states of the Mesopotamian Civilization, such as Ur, Uruk and Lagash, were located near the coastline of the Persian Gulf as is depicted in the map below.
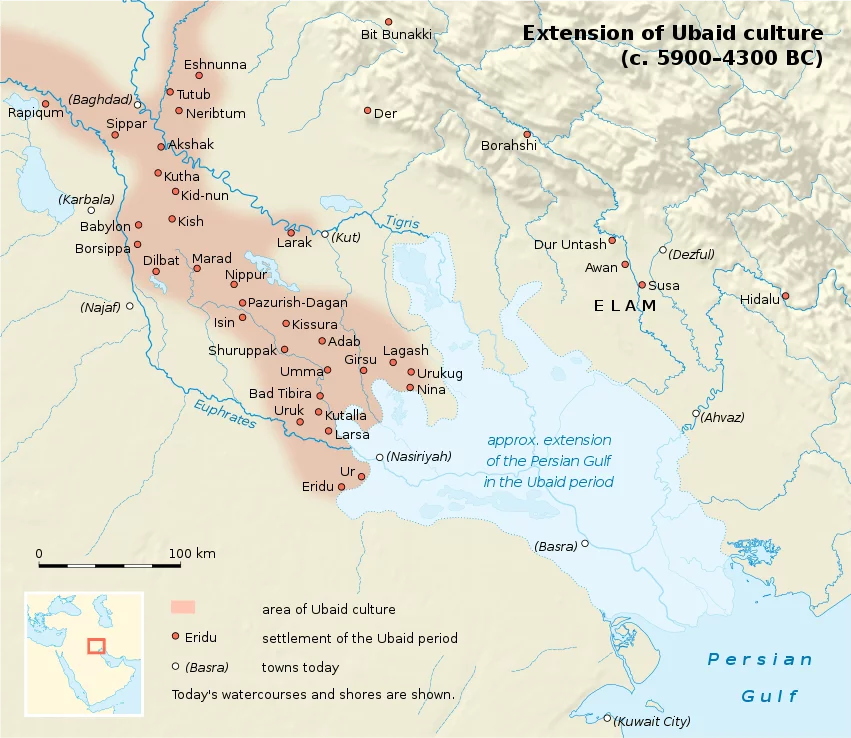
The Sumerians who settled near the coastline took interest in tidal oscillations caused by the Moon’s gravitational pull and therefore adopted the lunisolar calendar. On the other hand, the capitals of the Ancient Egypt, Memphis and Thebes, were located far from the coastline as the map below shows.
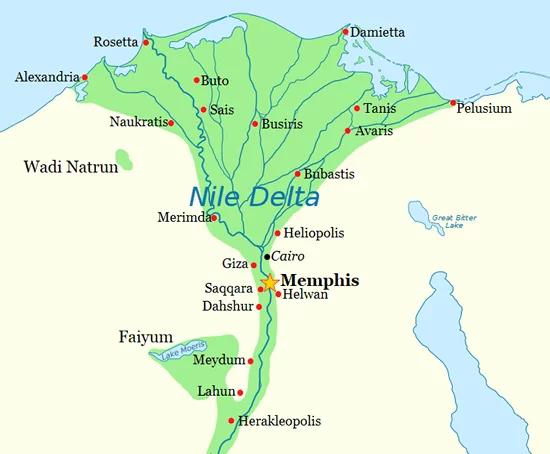
As the main concern of the Egyptians was not the monthly cycle of ebb and flow but the yearly cycle of the Nile’s inundation, the Egyptians adopted the solar calendar. The fact that they divided a year into the three seasons of akhet (inundation), peret (growth in winter) and shemu (harvest in summer) suggests how important the inundation of the Nile was for them.
So the bottom line is that the Sumerians attached greater importance to the lunar cycles than the Egyptians. Now that a synodic month has 30 days and a year without an intercalary month has 12 months, you might be tempted to say that “60 of sexagesimal is the least common multiple of 12 and 30[9]" .
Another interpretation of 12 and 30 is proposed by Stephen Kent Stephenson, who opposed the previous hypotheses as follows.
The divisibility of 60 was a convenient coincidental consequence, but not the primary reason the Sumerians adopted a sexagesimal number system. They did so from the periods of the two slowest moving of their seven sky gods. Jupiter and Saturn take 12 and 30 years, respectively, to track through the Zodiac. The observant Sumerians knew this. The least common multiple of 12 and 30 is 60.
In 60 years Jupiter would go through 5 cycles and Saturn 2. We have 5 fingers on each of 2 hands. In both cases 5+2=7, the number of sky gods. The mystical Sumerians would think of this as manifestations of the sky gods reflecting themselves in our anatomy.
The product of 12 and 30 is 360, the number of degrees in a circle; did the Sumerians define the 360-degree circle? Probably, because dividing the Zodiac into 360 degrees means Jupiter traverses 30 degrees in a year and Saturn 12 degrees, thereby coupling the periods of the gods Jupiter and Saturn.
The Sun tracks through the Zodiac in one year. Jupiter would track 1/12 of the way in that time. Why not divide a year into twelfths, i.e., 12 months; then the Sun tracks the same distance in one month that Jupiter tracks in one year; thereby coupling the periods of Jupiter and the Sun. And since the Sun would then track 30 degrees along the Zodiac in a month, why not divide the month into about 30 days, the period of Saturn? Then the Sun tracks about 1 degree every day.[10]
It is true that Babylonian astronomers systematically observed and recorded the movements of Jupiter and Saturn[11], but it is quite doubtful whether the discovery of the planetary cycles preceded the Sumerians’ invention of the sexagesimal system. Anyway Jupiter and Saturn conjoin every twenty years, and every third conjunction they are in the same zodiacal position as they were sixty years before. This fact, however, cannot be the ground for the Sumerian sexagesimal system. If the 60 year cycle of the conjunction is the ground, why didn’t they make the calendar of a 60-year cycle? The Sumerians must have known that a synodic month has 30 days and a year without an intercalary month has 12 months before they knew that the orbital period of Jupiter is 12 years and that of Saturn is 30 years. If you want to put forward the hypothesis that the base of the Sumerian sexagesimal system, 60, is the least common multiple of 12 and 30, you should find the ground in the former fact.
Of course, Mesopotamian astronomers must have recognized the numbers of 12 and 30 to be even more mysterious when they later knew the orbital period of Jupiter and Saturn, but this is not the primary reason that they divided a year into 12 months and the month into 30 days. It is not certain whether those who first defined the 360-degree circle were the Sumerians or the Greeks. Anyway the number 360 is based on the days in a lunisolar year without an intercalary month.
The number of the days in a week, namely seven, was also related to the lunar cycle. Babylonians and Hebrews celebrated the seventh day, because the phase of the Moon becomes the first quarter moon on the seventh day of a month[12]. When they later find the main celestial bodies (the Sun, the Moon, Mercury, Venus, Mars, Jupiter, and Saturn) are seven, they sanctified the number even more and the Westerners named each day of a week after them. In Latin, for example, Sunday, Monday, Tuesday, Wednesday, Thursday, Friday and Saturday are dies Sōlis, dies Lūnae, dies Martis, dies Mercuriī, dies Jovis, dies Veneris and dies Saturnī respectively, which obviously correspond to the names of the seven celestial bodies. But these names do not deny the lunar origin of the week.
It is true that Sumerians and Babylonians observed lunar cycles carefully and considered the number 12 and 30 important. But they did not adopt 60 as the base of their numerals because it is the least common multiple of 12 and 30. As Fig.02 shows, no special numerals are used to represent 12 and 30. We must recognize that the Sumerian sexagesimal system evolved from a decimal system. It is not the system of 12×30=60 but 10×6=60. The number 6, however, was not a significant number for Sumerians.
Later, the Pythagorean School regarded the number 6 as sacred, because it is the least perfect number. A perfect number is a positive integer that is equal to the sum of its proper positive divisors except the number itself and 6 is a perfect number since 1 + 2 + 3 = 6. But there is no evidence that Sumerians had such a belief. On the other hand, 12 was an important number, though not a perfect number, as is evident from their custom of dividing a year, a day and the zodiac into twelve sections. It is thought to be the legacy of the Sumerian Civilization that the numbers of Western languages up to 12 have names of their own and some units such as dozen and feet have 12 sub-units. If 12 is such an important number for Sumerians and their successors, why not regard 60 as the least common multiple of 10 and 12?
The following Venn diagram shows 60 belongs to the intersection of the multiples of 10 and 12.

10 is the number that humans can count simply on their fingers and 12 is the ratio of cycles of the two biggest celestial bodies. The sexagesimal system is located in the intersection of the decimal system and the duodecimal system, the earthly cycle and the heavenly cycle, the human order and the divine order. Kings of Mesopotamia, as the highest priest, took the role of mediating these two worlds. Using the sexagesimal system manifested their very existence. The Sumerians must have felt something mysterious in the proportion, 10:60=60:360, that is to say the number of fingers:60=60: days per year, because this proportion suggests that 60 is the mediating number that harmonizes the human order and the divine order.
3. Did the Stems and Branches originate in Mesopotamia?
If the Mesopotamian sexagesimal system can be interpreted in this way, it turns out to be a similar system to the Stems and Branches (Chinese: 干支; Pinyin: gānzhī) used in East Asian countries such as China, Japan, Korea and Vietnam for identifying hours, days, months, years and directions. It consists of 10 stems (Jia, Yi, Bing, Ding, Wu, Ji, Geng, Xin, Ren and Gui) and 12 branches (Zi, Chou, Yin, Mao, Chen, Si, Wu, Wei, Shen, You, Xu and Hai), thus forming a sexagenary cycle that starts with Jia-Zi. Did the Chinese sexagenary cycle derive from the Mesopotamian sexagesimal system?
3.1. The oldest form of the Stems and Branches
The oldest form of the sexagenary cycle is the method of recording days attested from the earliest written records in the Shang Dynasty (Chinese: 商朝; Pinyin: Shāng cháo), beginning ca. 1250 BC. We do not know for sure what this cycle was called in the era of the Shang dynasty. We can find the oldest name in the Discourses of the States (Chinese: 國語; Pinyin: Guóyǔ; written in 5th–4th century BC) and the Commentary of Zuo (Chinese: 春秋左氏傳; Pinyin: Chūnqiū Zuŏshìzhuàn; written in 4th century BC). The Discourses of the States described “10 Stems and 12 Branches (十干十二支)" as “10 Suns and 12 Movements (十日十二辰)" and the Commentary of Zuo wrote “The number of the Suns is 10." The Records of the Grand Historian (Chinese: 史記; Pinyin: Shǐjì; written from 109 to 91 BC) called it “10 Mothers and 12 Children (十母十二子)" in the era of the Western Han and the phrase “Stems and Branches" first appeared in the era of the Eastern Han. So, if you want to know what “10 Stems and 12 Branches" originally meant, you must understand what the oldest expression “10 Suns and 12 Movements (日之数、十)" implied.
The Ancient Chinese astronomers divided the celestial sphere into 12 sections from west to east in the direction of Jupiter’s revolution and called them “12 Successions (十二次)". They assigned the 12 Movements to the 12 Successions from east to west in the direction of diurnal motion. As the Movement of the year is decided in the relation to the Jupiter’s location which revolves in 12 years, Jupiter is called the “Year Star" (Chinese: 歲星; Pinyin: Suìxīng) and this year numbering system is called the “Year Star Calendar Era (歳星紀年法)" . Since the Year Star Calendar Era was mentioned in the Discourses of the States and the Commentary of Zuo, the 12 Movements these books mentions should be interpreted as 12-year cycle of Jupiter and the 10 Suns should be interpreted as 10 years. This interpretation enables us to assume that in the age of the Discourses of the States and the Commentary of Zuo Chinese had completed the theoretical basis for the Stems-and-Branches Calendar Era whose period is 60 years, though it did not become widespread until the age of the Han Dynasty.
This interpretation, however, raises a big problem. If such is the original meaning of “10 Suns and 12 Movements", why was it not the 60-year cycle from the beginning? The “10 Suns and 12 Movements" was first the 60-day cycle to identify a day in the era of the Shang Dynasty, then came to be used as the 60-year cycle to identify a year in the era of the Han Dynasty and also as the 60-month cycle to identify a month in the era of the Six Dynasties. The number of 12 means a year (12 months) in the 60-month cycle and the 12-year orbital period of Jupiter in the 60-year cycle, but it is not clear what it meant in the original 60-day cycle. Strangely enough the system that is more difficult to interpret was first adopted. Why was it so?
To solve this riddle, we must decipher the mysterious expression, “10 Suns and 12 Movements". Though we do not know for sure whether people of the Shang Dynasty used this expression, we can find oracle bone script (Chinese: 甲骨文; Pinyin: jiǎgǔwén) excavated among the ruins of the Shang Dynasty that corresponds to the characters of the current Stems and Branches. Some fortune-tellers interpret 10 Suns as 10 parts of a body and 12 Movements as 12 phases of fetal movements[13].
To be sure, the Shuowen (Chinese: 說文解字; Pinyin: Shuōwén Jiězì), an early 2nd century Chinese dictionary, presumes that 10 Stems (10 Suns) represent 10 parts of a body from head to legs.
| 10 Suns | Parts of a body and the explanation by Shuowen |
|---|---|
| jiǎ (甲) | The seams of skull “一曰人頭宐爲甲,甲象人頭。" |
| yǐ (乙) | The line from a chin to a throat “乙承甲,象人頸。" |
| bǐng (丙) | The shape of both shoulders “丙承乙,象人肩。" |
| dīng (丁) | The shape of a heart “丁承丙,象人心。" |
| wù (戊) | The shape of a chest “戊承丁,象人脅。" |
| jǐ (己) | The shape of intestines “己承戊,象人腹。" |
| gēng (庚) | The shape of an abdomen “庚承己,象人𪗇。" |
| xīn (辛) | The Y-shape of a crotch “辛承庚,象人股。" |
| rén (壬) | The I-shape of a leg bone “壬承辛,象人脛。" |
| guǐ (癸) | The X-shape of crossed legs “癸承壬,象人足。" |
The Shuowen assigns 12 Branches to 12 months and tries to interpret them as 12 phases of plants’ annual growth and death based on the doctrine of yin-yang (Chinese: 陰陽; Pinyin: yīnyáng) and the five elements. This interpretation of posterity deviates from the original meaning of 12 Movements but we can still find some points of contact with ours.
| 12 Movements | The phases of fetal movements and the explanation by Shuowen |
|---|---|
| zǐ (子) | Fertilization of an egg “十一月,陽气動,萬物滋。" |
| chǒu (丑) | Implantation on the uterine wall “十二月,萬物動,用事。象手之形。時加丑,亦舉手時也。" |
| yín (寅) | The modest differentiation of a stem cell “正月,陽气動,去黃泉,欲上出,陰尚彊。" |
| mǎo (卯) | The fetus drinks amniotic fluid and urinates. “二月,萬物冒地而出。象開門之形。" |
| chén (辰) | The first fetal movement “三月,陽气動,靁電振,民農時也。" |
| sì (巳) | Nutrition and oxygen through a navel string “四月,陽气巳出,陰气巳藏,萬物見,成文章,故巳爲蛇,象形。" |
| wǔ (午) | The fetus kicks against the womb. “五月,陰气午逆陽。冒地而出。" |
| wèi (未) | The limbs of the fetus branch out. “六月,滋味也。五行,木老於未。象木重枝葉也。" |
| shēn (申) | The fetus puts on height. “七月,陰气成,體自申束。" |
| yǒu (酉) | The body of the fetus gets mature. “八月黍成,可爲酎酒。象古文酉之形。" |
| xū (戌) | Nostrils and earholes are formed. The down is peeled off. “九月,陽气微,萬物畢成,陽下入地也。" |
| hài (亥) | The fetus is formed as a human. “十月,微陽起,接盛陰。" |
You might doubt whether the knowledge of the interior of the womb was available in the era of the Shang Dynasty, but Chinese at that time reportedly dissected pregnant women as a punishment and must have known it in this way.
If the 10 Suns and 12 Movements can be interpreted in this way, why was it later called so? First let us consider what the character “sun (日)" originally meant. According to Shuowen and Shiming (Chinese: 釋名; Pinyin: Shìmíng; written in c. 200 CE), “日" is equivalent to “實", a substance. The oracle bone script of “日" looks like a bar in a box, signifying the box is not void. So, we can safely say that 10 Suns meant 10 Substances of a body.
What’s about the 12 Movements? The “movement (辰)" has the same etymological origin as “swing (振)" and “shake (震)". As the phrase “star movement (星辰)" indicates, the word “辰" can mean heavenly bodies today, but because of its original meaning the heavenly bodies must have some periodic movements. Jupiter satisfies this condition and therefore 12 “辰" was interpreted as the 12 year cycle of Jupiter. On the other hand in the era of the Shang Dynasty “辰" of “十二辰" must have meant “娠", a character which is composed of a woman “女" and a movement “辰". So, the bottom line is the 10 Suns and 12 Movements signified the 10 substances of a body and the 12 phases of pregnancy.
Of course the character “日" had the current meaning of “day" as well and therefore the 10 Suns had to be 10 days long. To be adapted to this length, the 12 Movements became 12 days long and the 10 Suns and 12 Movements became the 60-day cycle that identified a day. When later Chinese converted the sexagenary cycle to the 60-year cycle that identified a year, the name became no longer appropriate and it was renamed the 10 Mothers and 12 Children or the 10 Stems and 12 Branches.
Now why the phases of pregnancy were divided into 12? As the 28-day human ovulation cycle is as long as the period of rotation and revolution of the Moon (月), it is called “menstruation (月經 the lapse of moon)". The English expression is derived from the Latin mēnsis (month), which in turn relates to the Greek μήνη (moon). This association can be found everywhere in the world. So, it is natural that the number of the pregnancy phases is the number that symbolizes the lunar cycle. The number of the body substances is, of course, based on the number of fingers. Thus the Chinese sexagenary has the same structure as the Sumerian sexagesimal in that 60 is the least common multiple of the number of fingers of both hands and the number of months in a year.
You might wonder why the number 28 was not adopted though the ovulation cycle and the period of rotation and revolution of the Moon are all 28 days. In fact this number is used for the Chinese constellations system, the Twenty-eight Mansions (Chinese: 二十八宿; Pinyin: èr shí bā xiù). This system divides the zodiacal band into 28 sections according to the movement of the Moon over a lunar month and allocates 28 constellations to them. The Moon migrates from constellation to constellation just as a traveler migrates from mansion to mansion. This is a system unique to China. I will take it up later.
The 10 substances of a body and the 12 phases of pregnancy in the Shang Dynasty was called the 10 Suns and 12 Movements in the Spring and Autumn or Warring States periods, the 10 Mothers and 12 Children in the Western Han Dynasty and the 10 Stems and 12 Branches in the Eastern Han Dynasty. The names of posterity just suggest that the 10 cycle is more fundamental than the 12 cycle, but the original sense remains in the 10 Mothers and 12 Children, that is to say, 10 completed substances and 12 phases in development. As Chinese write from top to bottom, 10 Stems are called the Heavenly Stems (Chinese: 天干; Pinyin: tiān gān) and 12 Branches are called the Earthly Branches (Chinese: 地支; Pinyin: dì zhī) especially in the Four Pillars of Destiny (Chinese: 四柱命理學; Pinyin: sì zhù mìnglǐ xué), but the relation of heaven and earth is reverse, because the stems sink deep roots in the earth while the branches reach out toward the heaven. As the 12 Branches reflect the period of the heavenly bodies (the Moon or Jupiter), it is absurd to call it the Earthly Branches. The original sense that the 10 Suns and 12 Movements had was forgotten with the times.
3.2. The 12 Branches and the 12 signs of the Zodiac
A theory that the Chinese 12 Branches derived from the Mesopotamian 12 zodiac constellations has been advocated by Guo Moruo (Chinese: 郭沫若; Pinyin: Guō Mòruò; November 16, 1892 – June 12, 1978)[14] and so on. To be sure there are some common features between them.
The first common feature is dividing a celestial sphere or a period into 12 sections. The Mesopotamian 12 constellations divide the zodiac, while the Chinese 12 Successions divide the celestial equator. But this is not a big difference. Like Babylonians Chinese adopted a lunisolar calendar, divided a year into 12 months, a day into 12 hours (Chinese: 時辰; Pinyin: shí chen) and applied the 12 Branches to them.
The second common feature is labeling at least the majority of 12 sections with names of animals. The Babylonians associated 12 constellations with 12 zodiac signs. The term “zodiac" stems from the Greek ζῳδιακὸς κύκλος meaning “circle of animals". The picture below shows that most of the zodiac signs are in fact animals.

Chinese also visualize the 12 Branches as 12 Animals (Chinese: 生肖; Pinyin: sheng xiào). The picture below shows that the Branches form a “circle of animals".

The third common feature is application to divination. Both the Babylonian horoscope and the Chinese Four Pillars of Destiny divine a person’s character and fortune based on the date of his or her birth in relation to the “circle of animals", though Four Pillars of Destiny do not ask where he or she was born.
The fourth common feature is the correspondence to the 12-year cycle of Jupiter. The Western astrologers believed a person’s fortune greatly changes when Jupiter transits the natal planet every 12 years. The Chinese astrologers imagine Tai Sui (Chinese: 太歲; Pinyin: tài suì), a mirror star of Jupiter that travels from east to west, that is to say, in the opposite direction to Jupiter and believed a person’s fortune greatly changes when his or her Branch is in alignment with Tai Sui every 12 years.
In spite of these common features, there are many differences between the Chinese 12 Branches and the Mesopotamian 12 zodiac signs. The biggest difference is that unlike the 12 zodiac signs the Chinese 12 Branches have no corresponding constellations. This difference, however, does not refute the hypothesis that the Chinese Branches derived from the Mesopotamian zodiac signs. As previously stated, China had established the original system of constellations called the Twenty-eight Mansions at the early Warring States period (770-221 BC). The system of the Twelve Successions that was introduced at the same time was inconsistent with the domestic system of the Twenty-eight Mansions. Why did China have two competing systems with the same function of dividing the celestial sphere and identifying constellations? In the end the Twelve Successions fell into disuse without taking the place of the Twenty-eight Mansions. So, it is likely the system of the Twelve Successions was imported to China from Mesopotamia.
How did the Mesopotamian astrology come to China then? Before explaining it, let me explain how it was propagated to Europe. According to The Histories by Herodotus, it was the Chaldean who brought astrology to Greece. The Chaldean, the people who founded the Neo-Babylonian Empire sought asylum in the West after the Persian Achaemenid Empire ruined the Neo-Babylonian Empire in 539 BC. They initiated the Greek into astrology about 4th century BC. This is about the same time when China introduced the 12 Successions and the Year Star Calendar Era. This fact suggests that the Chaldean refugees might have propagated their astrology to China as well as Europe.
3.3. The Stems and Branches originated in Mesopotamia
Although China is distant from Mesopotamia, China had been influenced by Mesopotamia since the prehistoric age. For example, the Yangshao Culture (Chinese: 仰韶文化; Pinyin: Yǎngsháo wénhuà; c. 5000-3000 BC) crafted pottery similar to that of Mesopotamia. It is no wonder that Mesopotamia had an influence on China in the historical age. The conclusion of this article is that the Chinese Stems and Branches originated in the Mesopotamian sexagesimal system. The propagation had two phases. The first phase is around 16th century BC, when the sexagesimal system was imported from the First Babylonian Dynasty to the Shang Dynasty and established as the sexagenary system composed of the 10 substances of a body and 12 phases of pregnancy. The second phase is around 4th century BC, when the astrological knowledge of horoscope was imported from the Neo-Babylonian Empire to the Eastern Zhou Dynasty and established as the 60-year cycle of the 10 Stems and 12 Branches where the number 12 was interpreted as the number of Jupiter instead of the Moon. Today both the Mesopotamian sexagesimal system and the Chinese sexagenary system are apt to be explained in terms of the 60-year conjunction cycle of Jupiter and Saturn, such an interpretation of posterity should not conceal the original implication of the Mesopotamian sexagesimal system and the Chinese sexagenary system.
4. References
- ↑Nancy Bowers."Kapauku numeration: Reckoning, racism, scholarship, and Melanesian counting systems." p. 105–116.
- ↑Bryan Derksen. “Grafisch vereinfachtes Zahlensystem der Mayas." Licensed under CC-BY-SA.
- ↑Josell7. “Números babilónicos." Licensed under CC-BY-SA.
- ↑前川 和也. 『メソポタミア文明』河出書房新社 (December 2, 2011). p. 72.
- ↑Johan G. van der Galiën. “A New Hypothesis about the Mesopotamium Sexagesimal." Version 1.3. September 25, 2005 (version 1.0. from August 13, 2002).
- ↑Samuel L. Macey. The Dynamics of Progress: Time, Method, and Measure. Univ of Georgia Pr (November 1, 2010). p. 92. Cf. Georges Ifrah. Histoire universelle des chiffres: L’intelligence des hommes racontée par les nombres et le calcul. Seghers; First Edition edition (1981).
- ↑NordNordWest. “Map of sites of the Ubaid culture." Licensed under CC-BY-SA.
- ↑Jeff Dahl. “Map of Ancient Egypt, showing the Nile up to the fifth cataract, and major cities and sites of the Dynastic period (c. 3150 BC to 30 BC).." Licensed under CC-BY-SA.
- ↑「十二進法 」日本語版ウィキペディア. 2012年12月8日 (土) 03:05 .
- ↑Stephen Kent Stephenson. “Ancient Computers." July 15, 2010. p. 19.
- ↑Sachs, Abraham. “Babylonian observational astronomy." Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 276.1257 (1974): 43-50. p. 45.
- ↑中山茂. 『西洋占星術―科学と魔術のあいだ』講談社 (June 1, 1992). p. 20-21.
- ↑波木星龍. 「十干十二支の変遷と真実の象形」Accessed on 20 Dec 2009.
- ↑成家徹郎. 「郭沫若の十二支起源研究」Accessed on 24 Jun 2016.
- ↑Talmoryair. “Byzantine mosaic of a Zodiac Wheel." Licensed under CC-BY-SA.
- ↑Jakub Hałun. “The carvings with Chinese Zodiac on the ceiling of the gate to Kushida Shrine in Fukuoka." Licensed under CC-BY-SA.







Discussion
New Comments
Wonderful research, thank you!
I would like to be convinced further that “But they did not adopt 60 as the base of their numerals because it is the least common multiple of 12 and 30.”
The selection of a base would be after noticing the cycles/circles/bases used by heaven by the earliest thinking cavemen – they would have assumed that heaven was counting in lots of 12, 30 and 360 – and therefore in lots and parts of 60.
It would have been beautiful, even, to think that the smallest whole number that both “months-per-year” and “days-per-month” can be divided into “days-per-year” is 60.
(The other, perhaps competing idea, is that once having determined a “heavenly” circle be divided into 360 equal degrees, the next perfect shape, the equal triangle, has angles of 60 degrees, dividing the major parts of the circle into 6 lots of 60 degrees, or 6 “hours” of 60 “minutes”).
Both these options seem simpler and more intuitive to me…
Thank you for comment.
To be sure, 12, 30 and 360 were as important numbers for Sumerians as 10 and I do not dismiss the fact that 60 is a multiple of 30 and a divisor of 360. But my question is why the Sumerian sexagesimal system evolved from the decimal system that they once used.
In addition to the explanation that I gave above, I can add another reason that 60 was significant for Sumerians. Maybe they must have felt something mysterious in the proportion, 10:60=60:360, that is to say the number of fingers:60=60: days-per-year.
This proportion suggests that 60 is the mediating number that harmonizes the human order and the divine order. Thus, as I wrote, “Kings of Mesopotamia, as the highest priest, took the role of mediating these two worlds. Using the sexagesimal system manifested their very existence.”
That is the interpretation by Otto Eduard Neugebauer (May 26, 1899 – February 19, 1990) . This fact might have justified the sexagesimal system afterward, but anyway it is derivative and not the original or essential reason they adopted the sexagesimal system.
The base 60 system comes from a much older system of mathematics based on something embedded in the digits of Pi
It is the basis of the entire system of Mesopotamian mathematical astronomy, and the reason behind the ” Great Pyramid ”
It predates Babylonia
Pure mathematical astronomy <== astrolatry <=== astrology <===religions
Start with the triangular figurate 2701, ie " Plato's number ", the knowledge of which Babylonians used as the basis of the mathematical value of the first verse of the Torah, a Babylonian fiction based on mathematical astronomy
It is first located in Pi at the ___ th through the ____th digits
The sum of ___ through ___ on the number line = 666
Nice website
Cheers
The value of Plato’s number is believed to be 216 = 63, which is the sum of the cubes for the simplest case of the Pythagorean Triple (3, 4, 5):
32 + 42 = 52.
Namely,
33 + 43 + 53 = 63.
60 is the product of the simplest case of the Pythagorean Triple.
60=3*4*5
Another suggestion for the importance of 60 is the 3600 = 602 year cycle of Nibiru, the twelfth Sumerian planet, which we can find in the ancient Sumerian cuneiform tablets dating back 6000 years ago.
Well, my friend
Plato was studying a remnant of something that was considered sacred in the ancient world, dating back to Uruk, and their system of mathematical astronomy
It pertains to some structures they found IN the digits of Pi in base 10 that are used to calculate movements in the Three-Body system
This knowledge was used in Sumerian / Babylonian / Akkadian gematria and became the basis for the Bible and the Genesis account
This would be a good place for you to start, something simple from my website
Also,….. there are no more than 5 planets listed in Sumerian cuneiform, ” neberu “, as it is properly pronounced, is recorded as appearing on a yearly basis { not every 3600 years }, Sumerians / Babylonians did not reckon orbits in base 10, or integer multiples, etc
It’s never described as a planet, it’s never described as being outside the solar system, in fact it is described as the ” place of crossing ” and refers to eclipse nodes in mathematical astronomy
It refers to the Sumerian city of Nippur, pronounced ” Ni-pu-ru “, containing the Garden of the Gods at Ekur, which was also based on the ” sacred ” mathematical information they held which was supposedly obtained from their god Enlil
Try looking in the MUL.APIN for ” niberu ” and see what you find :P
Mathematical astronomy and ancient mathematics / languages are my area of study
Please do not do everybody the disservice of merely regurgitating what you’ve heard, but rather delve into your studies so you speak the truth as well as possible
Thanks
Do you think Plato’s number has something to do with Sumerian sexagesimal numerals? Anyway, Sumerian sexagesimal numeral system seems to have little to do with Jewish decimal gematria.
Base-10 is the most natural numeral system to gravitate toward, because we have 10 digits on our hands. Yet there are other important number relationships that are displayed throughout the human body as well. One example being how a person’s head is proportionate to their overall height. At 2 months gestation, the fetus’ head is 1/2 the total body size. A newborn’s head is 1/4 of their total length, and a full-grown adult’s head will account for 1/8 of their height.
In addition to bodily proportions, I was inspired by DNA. The process of how binary cubes out closely resembles DNA’s processes of semi-conservative replication and binary fission. DNA is also sequenced using 4 different deoxynucletide triphosphates (dNTPs)- A, C, T and G.
Biology aside, hexadecimal highlights a some very interesting number relationships.
HEXADECIMAL
Row Properties
Row 1 – [ 0, 4, 8, C ]
Row 1’s numbers all contain 22 and are the main fractions of 16. 4=1/4, 8=1/2, C=3/4
Row 2 & 4 – [ 1, 5, 9, D ] and [ 3, 7, B, F]
The second and fourth rows are the odd rows. Most of the numbers are prime (1, 5, D, 3, 7, B) but they each row contains a single composite number (9 and F).
Row 3 – [ 2, 6, A, E ]
The third row- 2, 6, A , E – contains 2 multiplied by every odd-prime under 8. They account for all the x/8 fractions because of this.
2=2×1, 6=2×3, A=2×5, E=2×7
2=1/8, 6=3/8, A=5/8, E=7/8
BINARY
While less intuitive to write about, binary best illustrates the number relationships. Each column represents the first two binary digits, and each row represents the last two binary digits. Each “shape” has a corresponding “mark” with a matching value.
00 = 0 = Circle & Empty
01 = 1 = Up-Triangle & Dot
10 = 2 = Down-Triangle & Dash
11 = 3 = Square & Cross
How this portion works is where the inspiration from DNA really comes into play. These diagrams are the best way I have to describe my visualizations of the base-relationships and how the numbers form. I realize this part is long, so if you’re comfortable with the values of the cube you’re welcome to skip ahead to the portion on “Minimum Repeatable Patterns”.
Semi-conservative replication is the process where a single DNA strand while split in half, resulting in two daughter strands of DNA. Each of these daughter strands has one of its parents’ original strands. The original strands become the “parameters” for variation in the daughter strands, which are simply hybrids of the original information.
Binary would be the “parent strand” in this analogy. When referring to these parent strands I’ll write them out as Zero and One. Written this way, “One” does not represent a single digit value, but rather the idea of a binary chain of “1s” stretching on forever.
You could also think of it as “the largest single-digit value in a base”. In decimal, “One” would be 9. In hexadecimal it would be F.
Additionally, Zero is not treated as a non-value, but the origin-point. It represents space, emptiness and potential. One represents wholeness and generation. In a philosophical way, Zero equates to “Yin” and One to “Yang”.
Another good illustration for this idea is:
“We shape clay into a pot, but it is the emptiness inside that holds whatever we want” -Lao Tzu
The vase is One, the emptiness is Zero, all other numbers fill that vase.
Quaternary would be analogous to the “daughter strand” where each strand has a newly synthesized portion (Triangle) and an original portion (Circle and Square). The first “daughter” originates from 0- consisting of the circle “00” and up-triangle “01”. The second daughter comes from One, and consists of the square “11” and down-triangle “10”.
The change from quaternary to hexadecimal is better illustrated with Binary Fission. A cell will expand to accommodate all the information that’s being duplicated- this “expanding cell” represents the “base” used. Base-4 expands to Base-16 to allow the information to be copied.
The binary-quaternary relationship is similar, except 2 is copied and expanded into base-4.
Minimum Repeatable Pattern – MRP
Multiplication is where the cube’s relationships get really interesting. The model here shows what each of the components represents. From here, I further break down the pattern into “quadrants”. The beginning step in each quadrant is important to pay attention to.
Quadrant 0 = *0*, 1, 2, 3
Quadrant 1 = *4*, 5, 6, 7
Quadrant 2 = *8*, 9, A, B
Quadrant 3 = *C*, D, E, F
Each number has a 1, 2 or 4 mark sequence that repeats infinitely through all quadrants. These patterns always start on an empty mark. Dots and Crosses run in “opposite” directions of each other, and dashes alternate 0 and 1.
0.0.0.0 = Empty
0.01.10.1 = Dot
0.10.0.10 = Dash
0.1.10.01 = Cross
The beginning shape for each quadrant will correspond to the mark’s pattern. I tried turning the pattern in the image into a text matrix to make writing the pattern more understandable.
0 = Circle & Empty
1 = Square & Cross
01 = Up-Triangle & Dot
10 = Down-Triangle & Dash
The first row of the matrix is filled with the multiplicands. (0 – F )
The second row is the Mark pattern (1’s place)
The third row is the Shape Pattern (1’s place)
The fourth row is the Ten’s Mark Pattern (10’s place)
The fifth row is the Ten’s Shape Pattern (10’s place)
The | signifies the start of the next quadrant. If there is no mark in a row, that means that the mark or shape is being repeated.
You can see that the Mark Pattern (2nd row) goes 0.1.10.01
Now if you look at the Quadrant’s beginning shapes (column 0, 4, 8, C), the Shape pattern goes 0 – 1 – 10 – 01. The beginning-pattern is identical to its mark’s.
The shape pattern within the quadrant is unique though. For 3, the first shape repeats itself once, then the last shapes are
0.~.01.10 | 1.~.0.01 | 10.~.1.0 | 01.~.10.1 | …
I don’t have much experience writing formulas, but the sequence goes
“n, n, n+01, n+10”, with n being 0, 1, 01 or 10.
These overlaid patterns continue in tandem with each other infinitely, while the Ten’s place increases at it’s own, concurrent pace. Which is what this diagram illustrates:
This model shows the pattern for “5”. For all odd numbers, the 16-place-pattern will include every possible shape-mark combination. The Ten’s Place sequence will always resolve within the value of the given number. These sorts of patterns can be made with any squared-base (4, 9, 25…100). After the base sequence is input, your “10” repeats at the same interval as the “1”s. It’s hard to describe without getting too wordy, but if a further explanation is desired I’d be happy to go more in depth or provide clarification. My background is in art and biology, so mathematical writing is new to me.
Thank you for your time and assistance,
Ren Corrigan
It reminds me of the coherent superposition of a qubit (quantum bit). While classical computers use a bit (binary digit) whose state can only be either 0 or 1, quantum computers use a qubit whose state can be both until a measurement destroys its coherence. Thus a qubit has an unlimited number of possible values between 0 and 1. To use a visual illustration, it means you can insert a gradation of color between white and black.
While a DNA computer is a promising candidate for the next generation storage, a quantum computeris a promising candidate for the next generation computing. In the age of quantum computing, I proposed a modal logic or probability logic whose truth value can be anything between 0 and 1. See this article of mine for details, if you can read Japanese.
Do you aim at biological and fractal art like this?
I just looked up the qubit and how they work is fascinating! How quantum computers redirect and measure the horizontal and vertical polarization of light is interesting. Sometimes I use the numerals to graph out waves:
I haven’t read much Japanese since 2017, so it will take me some time to read through the article. I’ll respond to your proposed model in better detail separately. I can imagine how a Modal logic or Probability logic would work incredibly well within a quantum system though. It seems like you could have a super-state (of either 0 or 1) and a sub-state which is either inclusive/exclusive (“most”, “some”) using modal logic. Using probability logic the sub-state could be supportive/degradative (high/low probability) while inherently accounting for the total-value of the super-state. With the concept you’re using, would the qubit’s state be measurable without destroying its coherence? Especially with probability logic, it seems like you could track the state.
In regards to the qubits measurement/redirection using light though… I’d love to study more about the nature of light and how it interacts with the electro-magnetic field. Sunlight in particular is really unique. It can travel through thousands of miles through the vacuum of space, yet it nourishes us and so much of our natural world (plants, algae, etc.). Even how it interacts with the moon and the other planets in our solar system affects an untold number of systems on our planet- tides, hormonal rhythms, weather patterns, etc.
I do love fractal art! Most of my fractal + geometric work has been a byproduct of my numeral projects. The Fibonacci Sequence did spur a lot of my interest in biology though- Mollusks are one of my favorite groups of animals for how their shells develop. Normally I do concept art and life drawing. As an artist, it’s my duty to turn the ordinary into something extraordinary. There’s so much we take for granted in our natural world.
Preventing quantum decoherence is a challenging problem to put quantum computers to practical use. Technological problems aside, a modal logic or probability logic is still theoretically important to overcome the limits of binary logic.
In fact I can find fractals or self similarity in your figures.