シュメール人はなぜ六十進法を用いたのか
シュメール人が六十進法を用いたのは、60 に約数が多いからとか、60 まで両手で数える方法があるからとかいった理由からだけではない。60 は、両手の指の数である 10 と一年における月の朔望周期の回数である 12 との最小公倍数として意味のある数だからである。そして、この点のおいてメソポタミアの六十進法と六十年周期の中国の干支は同じ構造を持っており、後者は前者の文化的影響で成立したと推定できる。今日、メソポタミアの六十進法も中国の干支も、木星と土星が同じ黄道上の位置で合接する 60 年の周期で説明されることがあるが、それは占星術が発達した時代に考えられた解釈であり、そうした後世の解釈で本来の意味を見失ってはいけない。

1. メソポタミアの六十進法はどのようなものか
まずは、メソポタミア文明で用いられていた記数法と度量衡のシステムを概観することで、メソポタミア文明の六十進法がどのようなものであったか、またそれと度量衡がどのような関係であったかを確認したい。
1.1. メソポタミアの記数法
六十進法(Sexagesimal)とは、60 を底(てい base)として数を表す方法である。紀元前三千年頃にシュメール人によって世界初の位取り記数法として考案され、バビロニアに受け継がれ、周辺諸国の記数法にも影響を与えた。その影響は現在の世界にも及んでおり、時間や角度を表す時に部分的に六十進法が利用されている。現在私たちが用いている一般的な記数法は十進法であり、例えば、123 という数字は、1×102+2×101+3×100 と表されるが、1時2分3秒といった時間の表示では六十進法が用いられており、これを十進法で秒に換算すると、1×602+2×601+3×600=3723(秒)となる。
六十進法は、汎用的な記数法としては極めて特異であり、現在での使用例としては、ニューギニア島のエカリ語[1]ぐらいしかない。古代エジプトや古代ギリシャなど、世界の大部分では十進法が採用され、それが現代の標準となっている。人間にとって、指を折り曲げるのが最も自然な数え方であり、指の数が十本である以上、十進法は最も自然な記数法であるということになる。
マヤ文明などでは、二十進法が使われていたが、これは手足の指の数の合計が 20 であることによる。手も足も指の数は、一本につき五本であり、十進法や二十進法の記法の内部に五進法が含まれていることが多いのは、このためであると考えられる。例えば、以下の図は、マヤの記数法であるが、5 が準基(sub-base)であることから、手足の指を使って 20 を数えたことが容易に推測できる。たぶん、指一本が点一つで、手足一肢が横棒一本で表示されているのだろう。

シュメールの六十進法も、10 を準基としている。以下の図にあるように、縦の楔(V)が 1 を、横の楔(<)が 10 を表していて、59 に達するまでは十進法的に表記されている。実は、シュメール人は、紀元前3500年頃までは十進法を用いており、十進法から進化する形で六十進法に移行したのである。

なお、シュメールの数字にはゼロに相当する記号はなく、そのため、例えば、1 と 60 の区別が見た目ではつかず、文脈で判断するしかなかったが、それでは不便なので、古バビロニアの時代になってからは、位が空欄であることを示す記号が使われるようになった。
1.2. メソポタミアの度量衡
度量衡は必ずしも記数法を反映しない。例えば、英国は、十進法の記数法を用いているにもかかわらず、1971年2月13日まで 1ポンド = 20シリング、1シリング = 12ペンス という変則的な通貨単位を用いていた。メソポタミアの度量衡はそれに勝るとも劣らず変則的であった。ここでは、メソポタミアの度量衡を概観し、六十進法との関係を見ることにしたい。
まず長さであるが、六十進法では間が空きすぎるからなのか、中間的な単位が多数存在する。各単位間の比は 60 の約数や倍数になっており、六十進法で表記する上で都合が良いようになっている。
| 水準 | 比率 | メートル換算 | シュメール語 | アッカド語 |
|---|---|---|---|---|
| 大麦 | 1 | 1/360m | še | uţţatu |
| 指 | 6 | 1/60m | šu-si | ubānu |
| 足 | 2×60 | 1/3m | šu-du3-a | šīzu |
| 前腕 | 3×60 | 1/2m | kuš3 | ammatu |
| 歩 | 6×60 | 1m | ĝiri3 | šēpu |
| 葦 | 18×60 | 3m | gi | qanû |
| 棒 | 36×60 | 6m | nindan | nindanu |
| 綱 | 6×602 | 60m | eše2 | aslu |
次に面積の単位であるが、10 本の播種条を作った耕作面積の単位、1平方ニンダン(nindan)=1サル(sar)を基準として、次のように定められていた。
| 水準 | 比率 | 次元 | メートル換算 | シュメール語 | アッカド語 |
|---|---|---|---|---|---|
| 播種の基礎的単位 | 1 | 1 nindan × 1 nindan | 36m² | sar | mūšaru |
| 播種の単位 | 100 | 10 nindan × 10 nindan | 3,600m² | iku | ikû |
| 農地の単位 | 1,800 | 30 nindan × 60 nindan | 64,800m² | bur | būru |
ブル(bur)は正方形ではないが、これは耕作地が播種条に沿って縦長に割り当てられていた習慣による。サルとイク(iku)の関係は十進法的であるが、ブルとの関係では六十進法的な要素が入っていることがわかる。
次に体積であるが、6 シュシ(šu-si)の長さの 3 乗を 1 シラ(sila3)としていた。
| 水準 | 比率 | メートル換算 | シュメール語 | アッカド語 |
|---|---|---|---|---|
| 一杯 | 1 | 1/60L | gin2 | šiqlu |
| 一升瓶 | 60 | 1L | sila3 | qû |
| 一斗缶 | 10×60 | 10L | ban2 | sutū |
| 一桶 | 602 | 60L | ba-ri2-ga | parsiktu |
| 一樽 | 5×602 | 300L | gur | kurru |
これら体積の単位は、大麦の種子の量を測る単位として使われた。そして、1 ニンダンの長さの播種条に播く種の量は 1 ギン(gin2)、60 ニンダンの長さの播種条に播く種の量は 1 シラ、60 ニンダンの長さを持つ 1 ブルの面積の畑に播く種の量は 1 グール(gur)[4] というように、種の量と畑の面積は関連付けられていた。
最後に時間の単位であるが、1年が 12×30=360 日に分割され、さらに1日も 12×30=360 の下位単位に分割された。今日私たちは時間に関しては六十進法を用いているが、皮肉なことに、シュメール人たちは、時間に関しては三百六十進法を用いていたのである。
| 水準 | 比率 | メートル換算 | シュメール語 | アッカド語 |
|---|---|---|---|---|
| 分 | 1/360 | 240s | mu-eš | geš |
| 時 | 1/12 | 7,200s | da-na | bêru |
| 日 | 1 | 86,400s | ud | immu |
| 月 | 30 | 2,592,000s | itud | arhu |
| 年 | 360 | 31,104,000s | mu | šattu |
なお、一日が十二時間であったのはメソポタミア文明の初期の頃のことで、後には二十四時間に分割されるようになった。
2. メソポタミアで六十が特別視された理由は何か
なぜメソポタミア文明では六十進法が用いられていたのかに関してこれまで様々な説が出されているが、いまだに定説はない。ここで代表的な説を取り上げ、その妥当性を検討してみたい。
2.1. 高度合成数である
アレキサンドリアのテオン(Θέων; ca. 335 – ca. 405)以来、古くから指摘されている六十進法の利点は、約数の多さである。60 には、1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 と約数が 12 もあるので、分数の約分を比較的容易に行うことができる。以下のグラフを見ればわかるように、約数が 12 ある自然数は、60 以下にはない。60 よりも多くの約数を持つ最小の自然数は 120 までない。
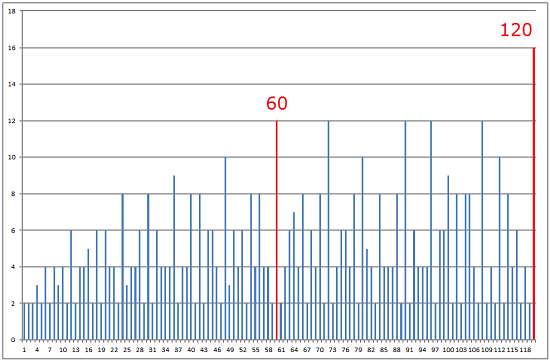
60 のように、それ未満のどの自然数よりも多くの個数の約数をもつものを高度合成数(highly composite number)という。高度合成数は、分割のしやすさゆえに度量衡に採用されやすい。ダースの 12 や角度の 360 も高度合成数である。既に確認したように、メソポタミアの度量衡には、60 の約数を単位とするものが多い。メソポタミアで神聖視された数字、7 が記数法の底として採用されなかった理由はこれで説明できる。
しかし、位取り記数法として最も使われている 10 は高度合成数ではないし、48 のように、比較的小さな高度合成数であっても、記数法の底として全く使われていない数もある。だから高度合成数であることは、位取り記数法の単位であるための必要条件でも十分条件でもない。たんに有利であるというだけのことで、60 でなければならない理由にはならないのである。
もっとも中には、60 がブレイクポイント以下の約数が最も多く連続している数[5]であるという点に着目してその必然性を導こうとする人もいる。すなわち、60 をその約数の積のペアで表すと、
となり、そのブレイクポイント、すなわち平方根
以下の約数は、1, 2, 3, 4, 5, 6 と連続する。12 も
というように、ブレイクポイント以下の約数が連続するが、六つ以上連続する自然数は 60 だけである。しかし、この数学的事実にどのような意味があるというのだろうか。たんに約数を全部書き並べる時に便利であるという以外のメリットはないのだから、六十進法が選ばれた決定的理由にはならない。後で述べるように、シュメール人は、12 という数字を重視していたので、12 がたんに 60 の約数であるのみならず、60 の約数の数でもあるということの特異性の方が重要であったように思われる。
2.2. 両手で数えられる
十進法が最もよく使われているのは、両手で数えることができるからである。同様に、六十進法も両手で数えることができるから用いられるようになったと言う人もいる。インドネシア、インド、パキスタン、アフガニスタン、イラン、トルコ、イラク、シリア、エジプトには、右手の親指で、右手の残りの四本の指の三つの骨を一つ一つ指しながら 3×4=12 を計算し、左手の指を一周するごとに一本折り曲げることで、12×5=60 を数えるという習慣がある[6]というのである。
だが、もしもこの数え方の習慣が理由で六十進法が誕生したとするならば、古代メソポタミアの記数法は、10 ではなくて、12 を準基としていたはずである。なぜ手で数える時は 12×5=60 なのに、文字で記す時は 10×6=60 にしなければならなかったのか。また、この習慣がある地域にはエジプトが含まれることにも注目したい。エジプトでは一般には十進法が用いられていたので、六十まで数える必要はなかったが、昼と夜を十二等分して時間を数えていたので、十二を数える需要があった。これらの事実を根拠に考えると、このカウント方法は、もともと十二を片手で数えるための方法であったが、後に六十を数える需要が出てきてから、もう一方の手で五を数えるようになったのであり、シュメールの六十進法はこのカウント方法とは独立に生まれたと推測できる。
なお、この方法で数えることができる最大の数は 60 ではない。左手で右手と同じことをすれば、122=144 まで数えることができる。つまり、十二進法で二桁まで手で数えることができる。両手でできるだけ大きな数を数えるという点を重視するなら、十二進法が最も合理的ということになるし、数えやすさを重視するなら、十進法になる。なぜシュメール人は、そのどちらでもない六十進法という中途半端な記数法を選んだのかが問われなければならない。
2.3. 天文学的な意味がある
エジプト文明が十進法であったのに対して、メソポタミア文明が六十進法であった理由を考える上で、両者の暦の差が参考になる。エジプト文明が太陽暦を採用していたのに対して、メソポタミア文明は太陰太陽暦を採用していた。太陰太陽暦とは、月の満ち欠けの周期である30日(より厳密には、29.53日なので、29日の月も混ぜなければならない)を1月とし、1年を12月とし、毎年11日ほど生じる回帰年とのずれを19年に7回の割合で閏月を挿入することで縮小する暦である。これに対して、エジプトの太陽暦は、1年を365日としており、暦の月と月相のサイクルは対応しない。メソポタミア文明が月の満ち欠けのサイクルを重視したのに対して、エジプト文明は太陽の回帰サイクルを重視したと言うことができる。
両者の違いは文明の中心地の所在の違いによって説明できる。メソポタミア文明の中心であったウル(Ur)、ウルク(Uruk)、ラガシュ(Lagash)は、以下の地図を見るとわかるように、当時は海岸のそばにあった。

海岸の近くに都市国家を形成した航海民族のシュメール人にとって、月の潮汐力による海面水位の変動は大きな関心事であり、それが暦にも反映されて、太陰太陽暦が作られたと考えられる。これに対して、以下の地図にあるように、古代のエジプト文明では、文明の中心(メンフィスあるいはテーベ)が内陸にあった。
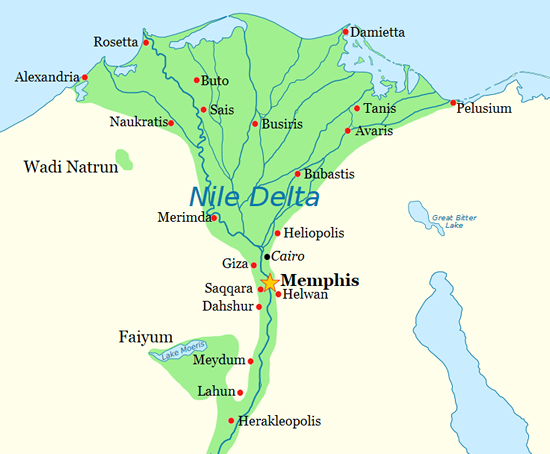
だからエジプト人にとっては、30日周期で起きる海岸での干満のサイクルよりも365日周期で起きるナイル川の氾濫の周期の方が予知するべき重大事であり、このため太陽暦が採用されたと考えられる。エジプトでは、一年が、洪水の季節(akhet)、種蒔きと成長の季節(peret)、収穫の季節(shemu)の三つの季節に分けられていたというのだから、ナイル川の水嵩の変動周期がいかに重要であったかがわかる。
以上を要するに、シュメール人は、エジプト人以上に太陽の回帰周期よりも月の朔望周期を重要視していたということである。朔望月は約30日であり、その周期は閏月のない一年に 12 ある。そこで、「六十進法の 60 は、12 と 30 の最小公倍数である[9]」という解釈がなされることがある。
但し、12 と30 という数字に別の周期を割り当てて六十進法を説明する人もいる。例えば、スティーブン・ケント・スティーブンソンは、次のような惑星周期に基づく仮説を立てている。
シュメール人の六十進法は、七つの空の神[太陽と月と五つの惑星]のうち最も動きが遅い二つ空の神[木星と土星]の運動周期から導かれたものだった。木星と土星が黄道帯を一周するのにそれぞれ12年と30年がかかる。観察力の鋭いシュメール人はこのことを知っていた。そして、12と30の最小公倍数は60である。
60年で木星は5回転、土星は2回転する。私たちは5本の指を2本の手に持つ。どちらの場合でも、5+2=7 と空の神の数になる。神秘的なシュメール人は、空の神が私たちの身体に具現したと思ったことだろう。
12×30=360 であり、これが角度の単位となった。おそらく、シュメール人は円の中心角を360°と定義したことだろう。なぜなら、木星は年に30°移動し、土星は12°移動するのだから、黄道帯を360°に分割することは、両者を結合することを意味するからだ。
太陽は黄道帯を一年で一周する。木星は同じ時期に太陽の1/12進む。それで1年は12月に分割された。そして、太陽は、木星が1年かけて移動する距離を1か月で進む。このように太陽と木星を関係付けるなら、その間太陽が黄道帯を30°移動するので、1月が30日に分割されるようになったと推測できる。30という数字は土星の周期の数字と同じであり、30に分割することで、太陽は毎日1°ずつ進むことになる。[10]
たしかに、メソポタミアで木星と土星の運動の観察が行われていたのは事実である[11]が、シュメール人が六十進法を使い始めたころから木星と土星の周期を知っていたかどうかははなはだ疑問である。それはともかくとして、木星と土星は 20 年ごとに合接するが、60年前と同じ黄道上の位置で合接するのは、三回目の合接においてである。しかし、それを根拠にシュメール人が六十進法を考案したとは考えられない。もしそうなら、六十年をサイクルとする暦を作ったはずだが、そういうことはなかったからだ。そもそも、朔望周期が30日で、それが1年に12回あるという事実は、土星の公転周期が30年で、木星の公転周期が12年であるという事実よりも先に知られていたから、30 と 12 の最小公倍数として 60 を位置付けるのであれば、前者が根拠となっていたはずだ。
もちろん、メソポタミアの天文学者は、太陽と木星の公転周期を後に知って、12 と 30 という数字に神秘的なものを感じたことだろうが、それを根拠に1年を12月に、そして1月を30日に分割ようになったということはない。黄道十二星座や黄道十二宮はメソポタミアが起源であるが、黄道(天球上における太陽の見かけの通り道)を12に分割し、毎月太陽が通過する12の星座を割り当てたことについても同じことが言える。角度を360に分割する習慣がシュメール文明の時代からあったかどうかは不明だが、明らかに、この数字は閏月のない太陰太陽暦の一年の日数が起源である。
週の日数である七という数字の起源も月の周期と関係がある。バビロニア人は、最初に半月(上弦の月)になる月の七番目の日を祭日にし、ヘブライ人も七番目の日を休日とし、ここから日曜日に休む習慣が生まれた[12]。後に主要天体が太陽と月と五つの惑星(火星、水星、木星、金星、土星)の合計で七つあることがわかると、七という数字はさらに神聖視されるようになり、日曜日、月曜日、火曜日、水曜日、木曜日、金曜日、土曜日というように、各曜日の名前に七つの天体(七曜)の名前を対応させるようになった。例えば、ラテン語では、dies Sōlis, dies Lūnae, dies Martis, dies Mercuriī, dies Jovis, dies Veneris, dies Saturnī というように、天体の名前がそのまま曜日の名前として使われたが、週の日数が本来は月の周期から生み出されたという事実を否定するものではない。
メソポタミア文明が月の周期を重視し、12 と 30 という数字に大きな意味を見出していたことは事実である。しかし、六十進法が使われるようになったのは、12 と 30 の最小公倍数が 60 であるからではない。なぜなら、シュメール/バビロニアの六十進記数法の図で確認できるように、12 も 30 も何ら特別な数字ではないからである。シュメール人の六十進法は十進法から進化したものであることを踏まえなければいけない。それは、10×6=60 というシステムなのである。しかし、シュメール人にとって、6 は直接重要な意味を持つ数字ではなかった。
後の時代の話になるが、ピタゴラス学派は、6を最小の完全数として神聖視していた。完全数とは、その数自身を除く約数の和が、その数自身と等しい自然数のことで、1 + 2 + 3 = 6 だから、6は完全数である。しかし、シュメール人が完全数を神聖視していたことを示す証拠はない。これに対して、12 は、完全数ではないが、一年のみならず、一日も黄道も 12 に分割していたことからもわかるように、シュメール人にとって重要な数字であった。今日にいたるまで、欧米語では 12 まで固有名を与えているし、フィートやダースなど十二進法の度量衡が使われているが、これはシュメール文明の影響である。12 がそれほど重要な数字だとするならば、六十進法の底である 60 は、10 と 12 の最小公倍数と位置付けなければいけない。
以下のベン図に示すように、60 の倍数の集合は、10 の倍数の集合と 12 の倍数の集合の積集合である。

10 は人間が指を折り曲げることで数える数字であり、12 は太陽と月という二大天体の関係を規定する数字である。六十進法は、十進法と十二進法が交差する位置、すなわち、地上の周期と天の周期、人間の秩序と神の秩序が調和する位置にある。そしてメソポタミアの社会において、この位置にいたのが神官、とりわけ最高の神官であったメソポタミアの王なのである。彼らにとって、六十進法を用いることは、自らの存在理由を示すことになるのである。一年の日数はおおよそ360日であり、10:60=60:360 という比の関係から、シュメール人は、60という数字を人間の秩序と神の秩序を調和させるマジックナンバーとみなしていたということも考えられる。
3. 干支の起源はメソポタミアにあるのか
メソポタミア文明の六十進法をこのように解釈するならば、それは、中国や日本などの周辺国で使われていた干支(十干十二支)に近いシステムとなる。干支とは、甲(こう)、乙(おつ)、丙(へい)、丁(てい)、戊(ぼ)、己(き)、庚(こう)、辛(しん)、壬(じん)、癸(き)という十干のサイクルと子(し)、丑(ちゅう)、寅(いん)、卯(ぼう)、辰(しん)、巳(し)、午(ご)、未(び)、申(しん)、酉(ゆう)、戌(じゅつ)、亥(がい)という十二支のサイクルを重ねることで得られる六十の周期で、年のみならず、時間や方位の同定にも用いられた。果たして中国の干支や十二支獣は、メソポタミアの六十進法や黄道十二星座を起源としているのであろうか。
3.1. 十日十二辰は十実十二娠だった
干支の最古の使用例は殷の時代に相当する紀元前1250年頃にまで遡る。殷墟出土の亀甲獣骨には、干支が、日付の特定のために印されている。但し、当時、干支というシステム自体が何と呼ばれていたのかは不明である。最も古い呼称は、春秋時代末期から戦国時代初期に書かれた書物である『国語』と『春秋左氏伝』に見られる。『国語』では、十干十二支は「十日十二辰」と記され、『春秋左氏伝』では「日之数、十」と書かれている。前漢の時代に相当する紀元前91年頃に書かれた『史記』では「十母十二子」と呼ばれており、「干支」という呼称が使われるようになったのは後漢の時代になってからのことである。だから、干支とは何かを知ろうとするなら、最古の呼称である「十日十二辰」が何を意味するのかを知らなければいけない。
古代の中国の天文学では、「十日十二辰」の「十二辰」は、天球の赤道帯を木星の移動方向である西から東に十二等分した十二次を東から西に向かう日周運動の方向に十二支を割り当てたもので、十二年で天球を一周する木星と十二辰との位置関係でその年の辰が決められた。木星は年を決める星ということで、歳星と呼ばれ、この紀年法は歳星紀年法と呼ばれた。歳星紀年法は『国語』や『春秋左氏伝』に見られるので、これらの書物が謂う所の「十二辰」は木星の周期で理解しなければならない。すると「十日十二辰」の「十日」は、太陽の周期である一年の十回分、すなわち十年ということになる。このように解釈することで『国語』や『春秋左氏伝』の時代に、後の漢の時代になって六十年周期で年を同定するために使われる干支紀年法の理論的基礎が出来上がっていたということができる。
しかし、この解釈には一つ大きな問題がある。もしも「十日十二辰」の意味がそういうものであるとするならば、なぜ十日十二辰は、最初から六十年の周期ではなかったのか。十日十二辰は、殷の時代には日を特定する六十日の周期であったが、漢の時代になると年を特定する六十年の周期となり、六朝時代には月を特定する六十月の周期にもなった。十二のサイクルは、六十月の周期では、十二月=一年の太陽の回帰サイクル、六十年の周期は木星の公転周期十二年に相当するが、六十日の周期では十二日が何に相当するのか不明である。にもかかわらず、よくわからないものほど早い段階で成立し。わかりやすいものほど後で成立しているのである。これはどういうことなのか。
この謎を解くためにも、殷の時代に使われていた十日十二辰がどういうものであったのかを考える必要がある。この時代に「十日十二辰」のような呼称があったかどうかはわからないが、「甲、乙、丙…」あるいは「子、丑、寅…」に相当する甲骨文字は出土している。そして、前者の十日を身体の十部位、後者の十二辰を胎児の十二の成長過程を記した象形文字であるという解釈[13]が提案されている。
まず十日(十干)であるが、『説文解字』によると、十干は身体の各部分を上から順番に象ったものである。『説文解字』は、甲骨文字が知られていなかった後漢の時代に書かれたものであるにもかかわらず、甲骨文字から推測される語源から懸け離れていない。
| 十日 | 身体の部位と『説文解字』での説明 |
|---|---|
| 甲 | 頭蓋骨の縫合線の象形。「一曰人頭宐爲甲,甲象人頭。」 |
| 乙 | 下顎から喉にかけての象形。「乙承甲,象人頸。」 |
| 丙 | 両肩とその肉の象形。「丙承乙,象人肩。」 |
| 丁 | 口の形。心臓の象形。「丁承丙,象人心。」 |
| 戊 | 胸の形象。「戊承丁,象人脅。」 |
| 己 | 腹の中の腸の象形。「己承戊,象人腹。」 |
| 庚 | へそのあたりの形。「庚承己,象人𪗇。」 |
| 辛 | 股の象形。「辛承庚,象人股。」 |
| 壬 | Iの形。すねの象形。「壬承辛,象人脛。」 |
| 癸 | Xの形。あぐらをかいだ両肢の象形。「癸承壬,象人足。」 |
次に、十二辰(十二支)の方だが、『説文解字』は、十二支を十二月に割り当て、陰陽五行説に基づいて草木の成長に合わせようとしているため、原義から逸れているものもあるが、原義と接点がないわけではない。
| 十二辰 | 胎児の成長段階と『説文解字』での説明 |
|---|---|
| 子 | 幼子としての受精卵が誕生する。「十一月,陽气動,萬物滋。」 |
| 丑 | 受精卵が着床し、子宮にしっかりしがみつく。「十二月,萬物動,用事。象手之形。時加丑,亦舉手時也。」 |
| 寅 | 受精卵が分化するが、まだつつましい状態。「正月,陽气動,去黃泉,欲上出,陰尚彊。」 |
| 卯 | 開門。胎児が羊水を飲んだり排尿したりする。「二月,萬物冒地而出。象開門之形。」 |
| 辰 | 振動。胎児が動き始める。「三月,陽气動,靁電振,民農時也。」 |
| 巳 | 臍の緒を通じて母から栄養と酸素をもらう。「四月,陽气巳出,陰气巳藏,萬物見,成文章,故巳爲蛇,象形。」 |
| 午 | 逆らう。胎児が子宮を蹴るようになる。「五月,陰气午逆陽。冒地而出。」 |
| 未 | 手足が枝のように伸び始める。「六月,滋味也。五行,木老於未。象木重枝葉也。」 |
| 申 | 胎児の身長が伸びる。「七月,陰气成,體自申束。」 |
| 酉 | 皮下脂肪が付き、胎児の身体が成熟する。「八月黍成,可爲酎酒。象古文酉之形。」 |
| 戌 | 削る。鼻や耳の穴が開通する。毳毛が剥落する。「九月,陽气微,萬物畢成,陽下入地也。」 |
| 亥 | 胎児の人としての形が定まる。「十月,微陽起,接盛陰。」 |
殷の時代にこれらの胎内に関する知識があったことを疑う人もいるだろうが、中国では殷の時代から「剖腹(ほうふく)」の刑が行われていたと伝えられるので、そうした方法で胎内に関する知識を得ていたものと考えられる。
殷の時代における十日十二辰が以上のようなものであるとするならば、なぜそれは後に「十日十二辰」と呼ばれるようになったのか。まずは、「日」という漢字の本来の意味を考えてみよう。今日ではもっぱら太陽を意味する字となっているが、『説文解字』や『釋名』によると、日(じつ)は實(実 じつ)である。「日」は、甲骨・金文では、四角の枠の中に小点を加えた形をしており、空っぽではないことを示す記号となっている。つまり「十日」は「十実」であって、身体を構成する十の実体という意味だったと解釈できる。
では「十二辰」はどういう意味なのか。「辰」は「振」や「震」と同じで、「振れる、震える」という意味である。「星辰」という熟語があることからもわかるように、天体という意味でも今日使われるが、原義との関係で言うと、振れながら同じことを繰り返す周期を持つ天体でなければならない。木星はこの条件を満たしており、だから、「十二辰」は木星の十二年周期と解釈されるようになったのだが、殷の時代の「十二辰」はそうではなかった。殷の時代の「十二辰」は、むしろ「十二娠」だった。「娠」は、女偏に「辰」だから、胎児が女の腹の中でうごめくことを意味する。そのプロセスを十二の時期に分割したものが「十二娠」だったと解釈できる。「十日十二辰」は、殷の時代では「十実十二娠」であったというのが私の仮説である。
もちろん「十日十二辰」の「日(じつ)」には、「実」以外にも「日(にち)」という意味もある。「十日」が10日の長さなら、それに合わせて「十二辰」は12日の長さとなり、「十日十二辰」は両者の最小公倍数である60日の長さとなる。「十日十二辰」が、日を特定するための六十日周期のシステムであった理由はこのように説明できる。そして、後に「十日十二辰」という呼称が使われなくなった理由も、他の長さの周期、例えば六十年周期にも使えるようにするためだったと説明することができる。
ところで、妊娠の段階は、なぜ十二に分けられたのだろうか。女性の子宮の排卵周期は、月の自転周期=公転周期である二十八日とほぼ同じなので「月経(月の経過時間)」と呼ばれる。英語では、“menstruation”と言われるが、これも月を意味するラテン語の“mēnsis”あるいはギリシャ語の“μήνη”に由来する。この連想は世界各地に見られる。だから、月の周期を象徴する数字である十二で段階分けされたと考えるのが自然である。「十実」の十はもちろん人間の指の数である。してみると、中国の十実十二娠は、指の数の十と一年における月の数の十二から構成されており、シュメールの六十進法と同じ構造を持っていることがわかる。
二十八日が月の自転周期=公転周期であり、月経の周期でもあるのに、なぜ二十八という数字が採用されなかったのかと疑問に思う人もいることだろう。実は、二十八という数字は、中国では二十八宿という形で使われている。二十八宿とは、月の通り道(白道)を二十八のエリアに分割した天球分割法ないしそのエリアに一つずつ存在する二十八の星座のことである。月の公転周期が二十八日であるので、月は一日に白道上の星座を一つずつ移動することになる。それはまるで旅人が毎日宿に泊まるようなので、各星座は宿と呼ばれた。これは中国独自の月信仰の結実である。二十八宿については、また後で取り上げる。
話を十実十二娠に戻そう。このシステムは、春秋戦国時代に十日十二辰となり、前漢時代には十母十二子となり、後漢時代には十干十二支となった。十母十二子は、十の周期の方が十二の周期よりもより基本であることを示しているが、十実十二娠の元の意味を残していると見ることができる。すなわち、十実は、完成した母の人体における十の実体を表し、十二娠は、完成するまでに子が辿る十二の発展段階を表していると解釈できる。しかし、十干十二支では、十の周期は幹(干)で、十二の周期は枝(支)ということだから、たんに前者が後者よりも重要であるということしか意味しない。宋の時代以降に成立した四柱推命(八字命學)では、縦書きで干が上で支が下であることから天干地支と呼んでいるが、幹は地面に根差し、枝は天に向かって伸びているのだから、天地との関係が逆になっている。特に十二支は、月であれ、木星であれ、天体の周期だからそれを地支と言うのはおかしい。十実十二娠は、時代とともにその本来の意味が忘れられていったのである。
3.2. 十二支と黄道十二宮を比較する
中国の十二次や十二辰がメソポタミア起源の黄道十二宮に由来するという説は、これまで郭沫若などによって唱えられてきた[14]。たしかに両者にはいくつかの共通点がある。
最初の共通点は、天球や時間を十二に分割するというところにある。メソポタミアの黄道十二星座では分割対象が黄道帯であるのに対して、中国の十二次では天の赤道帯という違いがあるものの、天球を十二等分しているという点では同じである。時間の分割に関しても、中国はメソポタミアと同様に、太陰太陽暦を採用し、一年を十二月としたのみならず、一日を十二等分し、各二時間の十二の時辰に十二支を割り当てた。
第二の共通点は、動物を主とする十二のキャラクターが象徴として使われるところにある。メソポタミアでは十二に分割された黄道のそれぞれに十二の星座が割り当てられ、黄道十二宮として記号化された。黄道十二宮(zodiac signs)はギリシャ語の“ζῳδιακὸς κύκλος”に由来するが、これは獣環、つまり動物のサークルという意味である。以下の図では、文字通りサークル内に十二宮が配置されているが、その大半が動物であることが確認できる。

日本ではおなじみのことであるが、中国とその周辺国で普及した十二支にも、十二匹の動物、すなわち十二生肖(じゅうにせいしょう)が割り振られている。以下の図は、方角と十二生肖を対応させたもので、これまた「動物のサークル」となっている。

第三の共通点は、生まれた時、十二のセクションのどこに属するかで個人の運勢が占われたというところにある。サイン(黄道十二宮)を用いたバビロニア起源の西洋占星術(ホロスコープ)も、干支を用いた中国起源の四柱推命も、その占い方に違いがあるものの、生まれた年月日時をもとに占うという点では、同じである。西洋占星術を簡略化したものとして星座占いがあるが、中国にも、四柱推命よりも簡単な干支占いがある。
第四の共通点は、木星の十二年周期との対応である。木星は黄道十二宮間を毎年一つずつ移動する。西洋占星術では、人の運命はその人のサインに木星が位置する時に大きく変わると信じられている。中国の天球では、木星は十二次を西から東に一次ずつ進むが、十二支の向きはこれとは逆であるため、東から西に進む仮想の惑星、太歳(たいさい)を木星の鏡像体として想定し、人の吉凶は、その人の干支が太歳の方位に当たる年に極端に現れると信じられている。
メソポタミアの黄道十二宮と中国の十二支には以上のような共通点があるものの、相違点もたくさんある。なかでも、中国の十二支が対応する星座を持たないという点は最大の相違点と言われている。しかし、これは十二支がメソポタミア起源であることを否定するものではない。既に述べたように、中国には、二十八宿という、天球を分割し、星座を位置付ける独自の方法が戦国時代初期には完成していた。同じ時期に導入された十二次は、二十八宿とは整合的ではなく、競合する関係にあり、中国が、両立しない二つのシステムを同時期に自ら作ったとは考えにくい。結局のところ、十二次は星座同定方法としては二十八宿に取って代わることなく廃れてしまった。それゆえに、十二次や十二辰は、中国の習慣を無視して入ってきた外来のシステムと考えられる。そしてその起源は、メソポタミア以外には考えられない。
では、メソポタミアの黄道十二宮はどのようにして中国に伝わったのだろうか。それを説明する前に、バビロニアの占星術がどのようにしてヨーロッパに伝わったのかを説明しなければならない。ヘロドトスの『歴史』などによると、ギリシャに占星術や天文学の知識をもたらしたのは、カルデア人という東方の賢人で、それゆえ、それらの知識は「カルデアの知恵」と呼ばれた。カルデア人とは新バビロニアを建国した人々で、紀元前539年にアケメネス朝ペルシアに滅ぼされると、その遺民たちが西方に亡命し、紀元前四世紀頃にギリシャに「カルデアの知恵」を伝えた。そして、中国で周天を十二次に分割し、木星の位置によって年を記す歳星紀年法が成立したのも紀元前四世紀頃なのである。それならば、カルデア遺民の一部は、中国にまで来て、「カルデアの知恵」を伝えたと推定することはできないだろうか。
3.3. 干支の起源はメソポタミアにある
メソポタミアと中国は距離的に離れているが、メソポタミアの彩陶と類似の土器が仰韶(ぎょうしょう)文化の遺跡から発掘されるなど、中国は先史時代からメソポタミアの文化的影響を受けていたと推測される。殷は戦車を採用した最初の中国王朝であるが、車輪の起源はメソポタミアなので、殷がメソポタミアと接触していた可能性は極めて高い。中国の干支はメソポタミアの影響で成立したというのが本稿の結論であるが、それは一度に成立したのではなくて、二つの段階を経て成立したと考えられる。第一段階は殷が成立した紀元前十六世紀頃で、この時、古バビロニア王朝から中国に六十進法が伝わり、十実十二娠が六十日周期のシステムとして成立した。第二段階は紀元前四世紀頃の春秋戦国時代で、この時、新バビロニア王朝から中国に黄道十二宮や占星術の知識が中国に伝わり、十二という数字が、一年における月の数ではなくて、木星の公転周期と解釈されるようになり、六十年周期の十干十二支が干支の主流となった。今日、メソポタミアの六十進法も中国の十干十二支も、後の時代の発見である木星の公転周期で解釈されがちだが、そうした解釈で本来の意味を見失ってはいけない。
4. 参照情報
- ↑Nancy Bowers."Kapauku numeration: Reckoning, racism, scholarship, and Melanesian counting systems." p. 105–116.
- ↑Bryan Derksen. “Grafisch vereinfachtes Zahlensystem der Mayas.” Licensed under CC-BY-SA.
- ↑Josell7. “Números babilónicos.” Licensed under CC-BY-SA.
- ↑前川 和也. 『メソポタミア文明』河出書房新社 (December 2, 2011). p. 72.
- ↑Johan G. van der Galiën. “A New Hypothesis about the Mesopotamium Sexagesimal." Version 1.3. September 25, 2005 (version 1.0. from August 13, 2002).
- ↑Samuel L. Macey. The Dynamics of Progress: Time, Method, and Measure. Univ of Georgia Pr (November 1, 2010). p. 92. Cf. Georges Ifrah. Histoire universelle des chiffres: L’intelligence des hommes racontée par les nombres et le calcul. Seghers; First Edition edition (1981).
- ↑NordNordWest. “Map of sites of the Ubaid culture.” Licensed under CC-BY-SA.
- ↑Jeff Dahl. “Map of Ancient Egypt, showing the Nile up to the fifth cataract, and major cities and sites of the Dynastic period (c. 3150 BC to 30 BC)..” Licensed under CC-BY-SA.
- ↑「十二進法 」日本語版ウィキペディア. 2012年12月8日 (土) 03:05 .
- ↑“The divisibility of 60 was a convenient coincidental consequence, but not the primary reason the Sumerians adopted a sexagesimal number system. They did so from the periods of the two slowest moving of their seven sky gods. Jupiter and Saturn take 12 and 30 years, respectively, to track through the Zodiac. The observant Sumerians knew this. The least common multiple of 12 and 30 is 60. In 60 years Jupiter would go through 5 cycles and Saturn 2. We have 5 fingers on each of 2 hands. In both cases 5+2=7, the number of sky gods. The mystical Sumerians would think of this as manifestations of the sky gods reflecting themselves in our anatomy. The product of 12 and 30 is 360, the number of degrees in a circle; did the Sumerians define the 360-degree circle? Probably, because dividing the Zodiac into 360 degrees means Jupiter traverses 30 degrees in a year and Saturn 12 degrees, thereby coupling the periods of the gods Jupiter and Saturn. The Sun tracks through the Zodiac in one year. Jupiter would track 1/12 of the way in that time. Why not divide a year into twelfths, i.e., 12 months; then the Sun tracks the same distance in one month that Jupiter tracks in one year; thereby coupling the periods of Jupiter and the Sun. And since the Sun would then track 30 degrees along the Zodiac in a month, why not divide the month into about 30 days, the period of Saturn? Then the Sun tracks about 1 degree every day." Stephen Kent Stephenson. “Ancient Computers." July 15, 2010. p. 19.
- ↑Sachs, Abraham. “Babylonian observational astronomy." Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 276.1257 (1974): 43-50. p. 45.
- ↑中山茂. 『西洋占星術―科学と魔術のあいだ』講談社 (June 1, 1992). p. 20-21.
- ↑波木星龍. 「十干十二支の変遷と真実の象形」Accessed on 20 Dec 2009.
- ↑成家徹郎. 「郭沫若の十二支起源研究」Accessed on 24 Jun 2016.
- ↑Talmoryair. “Byzantine mosaic of a Zodiac Wheel.” Licensed under CC-BY-SA.
- ↑Jakub Hałun. “The carvings with Chinese Zodiac on the ceiling of the gate to Kushida Shrine in Fukuoka.” Licensed under CC-BY-SA.

















ディスカッション
コメント一覧
シュメールは十進法も使っていた。
シュメールの考古学本で、読んだ記憶がありますが。
併用していたのでは?
そうです。そしてそれは本文に既に書いてあります。該当箇所を引用しましょう。
読み落としていました。失礼!
“The divisibility of 60 was a convenient coincidental consequence, but not the primary reason the Sumerians adopted a sexagesimal number system. They did so from the periods of the two slowest moving of their seven sky gods. Jupiter and Saturn take 12 and 30 years, respectively, to track through the Zodiac. The observant Sumerians knew this. The least common multiple of 12 and 30 is 60. In 60 years Jupiter would go through 5 cycles and Saturn 2. We have 5 fingers on each of 2 hands. In both cases 5+2=7, the number of sky gods. The mystical Sumerians would think of this as manifestations of the sky gods reflecting themselves in our anatomy. The product of 12 and 30 is 360, the number of degrees in a circle; did the Sumerians define the 360-degree circle? Probably, because dividing the Zodiac into 360 degrees means Jupiter traverses 30 degrees in a year and Saturn 12 degrees, thereby coupling the periods of the gods Jupiter and Saturn. The Sun tracks through the Zodiac in one year. Jupiter would track 1/12 of the way in that time. Why not divide a year into twelfths, i.e., 12 months; then the Sun tracks the same distance in one month that Jupiter tracks in one year; thereby coupling the periods of Jupiter and the Sun. And since the Sun would then track 30 degrees along the Zodiac in a month, why not divide the month into about 30 days, the period of Saturn? Then the Sun tracks about 1 degree every day.” Stephen Kent Stephenson. “Ancient Computers.” July 15, 2010. p. 19.