ゼロから始まる暦の提案
現在私たちが使っているグレゴリオ暦や西暦にはゼロが存在しない。だから、ゼロ年やゼロ月やゼロ日はない。これは西暦やグレゴリオ暦の原型であるローマ暦が最初に考案された当時のヨーロッパでは、ゼロという数字がなかったからである。しかし、今日私たちが用いている十進法はゼロベースであり、ゼロベースではない付番システムで時点を同定すると、時間を変数とした演算がやりにくくなる。伝統的なシステムをむやみに変更するべきではないが、数学が後進的であった時代のヨーロッパで作られた時間システムに人類がこれからも拘束され続けることは好ましいことではない。そこで、暦をゼロベースにするにあたって、どのような暦にすれば最も理想的になるかを考えてみよう。

目次
1. ヨーロッパの暦にはなぜゼロがないのか
現在世界で最も広く使われている紀年法である西暦にゼロ年は存在しない。紀元一年(AD 1)の前の年は、紀元ゼロ年ではなくて、紀元前一年(1 BC)である。同じことはヨーロッパの紀年法のみならず、暦法に関してもあてはまる。世界の暦のデ・ファクト・スタンダードとなったローマ暦の現代版、グレゴリオ暦にも、ゼロ月やゼロ日も存在しない。なぜなら、6世紀のローマの神学者、ディオニュシウス・エクシグウス(Dionysius Exiguus; c. 470 – c. 544)が西暦を考案した当時、さらには、グレゴリオ暦の前身であるユリウス暦が導入された紀元前46年当時のヨーロッパの記数システムにはゼロがなかったからである。もっとも位取り表記で空欄を表す記号なら、古代バビロニアの時代から存在した。エクシグウスも“nulla”という言葉を「無」を表す文字として使っていた。しかし、それは数字のゼロとは異なる[1]し、だからヨーロッパの時間軸にゼロという時点は存在しなかった。古代ローマのみならず、それも学問的水準が高かった、そして西欧文明の源泉となった古代ギリシアにも数字としてのゼロはなかった。
これに対して、記数システムにゼロがあったマヤとインドは、ゼロ年を起点とする紀年法と暦法を作ることができた。マヤの長期暦は、グレゴリオ暦の紀元前3114年をゼロ番目の年、そしてその年の8月11日をゼロ番目の日とし、その日を起点に2012年12月21日まで作成されていた。主要な循環暦としては、20日×18月+5日=365日を一年とする「ハアブ暦(Haab’ Calendar)」が使用されていたが、日の数え方はマヤの一般的な記数法である二十進法に従っており、各月は「着座」と呼ばれた0日から始まり、19日で終わる。インドの「カリ・ユガ(कलियुग)」は、グレゴリオ暦の紀元前3102年1月23日午前0時をゼロ年ゼロ日の基準時点としており、天文学的な計算は、そのゼロ時点からの「積日(アハルガナ अहर्गण)」で計算された。
では、なぜ古代ギリシアの数学は、当時世界最高水準にあったのにもかかわらず、ゼロを記数システムに取り入れることができなかったのか。それは古代のギリシア人が無の存在を認めなかったからだ。ギリシアにももちろん「メーデイス(μηδείς)」という「無」に相当する言葉はあったが、ギリシア人はその言葉の対象が実在するとは思わなかった。パルメニデス(Παρμενίδης ὁ Ἐλεάτης; fl. early 5th century BC)やプラトン(Πλάτων; 424/423 BC – 348/347 BC)が典型的にそうであったように、ギリシャ人は真空が実在するとは考えていなかったのである。アリストテレスは、『自然学』において、空間が希薄になると周囲からの流入が生じるという理由から、真空は存在しえないと主張した[2]。その後、アリストテレスのこの説から「自然は真空を嫌う(horror vacui)」という格言が生まれたが、自然にそうした感情があるわけではないのだから、この擬人的表現は、ヨーロッパ人の真空に対する嫌悪感を対象に投射したものであると解釈するべきである。
古代ギリシアには、真空の存在を肯定する哲学者たちもいた。レウキッポス(Λεύκιππος)やデモクリトス(Δημόκριτος; ca. 460 – ca. 370 BC)などの原子論者は、彼らがアルケーとみなす原子(ἄτομος)が自由に運動する空間として空虚(κενός)の存在を想定した。しかし、彼らの原子論は当時のギリシアでは受け入れられなかった。ディオゲネス・ラエルティオスの『ギリシア哲学者列伝』には、プラトンが、デモクリトスの虚空論をいかに嫌悪したかを物語る次のようなエピソードを紹介している。
プラトンは、集めることができたかぎりのデモクリトスの書物を燃やしてしまおうとしたが、ピュタゴラス派のアミュクラスとクレイニアスが、それらの書物はすでに多くの人たちに出回っているのだから、そのようなことをしても何にもならないと言って、プラトンに思いとどまらせたとアリストクセノスが『歴史覚書』の中で書いている。[3]
デモクリトスの書物を抹殺することを断念したプラトンは、デモクリトスを徹底的に無視することで彼を哲学史から抹殺しようとした。プラトンは著作の中で多くの同時代の哲学者について語ったのにもかかわらず、デモクリトスには全く言及することはなかった。あたかも自然が真空を嫌悪するがごとく、プラトンはデモクリトスの無の思想を嫌悪し、無の思想を無視することでそれを文字通り無にしようとした。そうしたプラトンの努力が実ってか、古代ギリシアの原子論は、その後忘れ去られるようになった。ヨーロッパ人が真空の実在を認めるようになったのは、1643年のトリチェリ(Evangelista Torricelli; 15 October 1608 – 25 October 1647)の水銀柱を用いた実験以降である。また、1648年に、パスカル(Blaise Pascal; 19 June 1623 – 19 August 1662)は、真空を生じさせる水銀柱の高さが、水銀の重さと釣り合う空気の重さによって決まることを認識し、「自然は真空を嫌う」という擬人的仮説を否定した。
『ミリンダ王の問い』からもわかるように、ヨーロッパの主流が有の思想であるのに対して、インドの主流は無の思想である。例えば、ジャイナ教は、物質の構成要素としてパラマーヌを、さらに、パラマーヌが存在する虚空としてアーカーシャを想定する原子論的な存在論を提示していた。ジャイナ教の開祖であるマハーヴィーラ(महावीर; 599/444 BC? – 527/372 BC?)は、生没年がはっきりしないが、レウキッポスやデモクリトスなどのギリシアの原子論者より前の時代の人物と推定される。仏教の開祖である釈迦(सिद्धार्थ गौतम बुद्ध; 463 BC? – 383 BC?)も生没年がはっきりしないが、その思想が倫理思想をも含めて仏教に近いエピクロス(Ἐπίκουρος; 341 BC – 270 BC)よりも前と考えられる。だから、実証はできないが、レウキッポスやデモクリトスがジャイナ教の形而上学の影響を受けたとか、エピクロスが仏教の影響を受けたといった可能性がある。
いずれにせよ、無の思想は、インドでは主流になりえたが、ヨーロッパでは異端として排除される運命にあった。だから、ヨーロッパよりもインドが先にゼロを数学に取り入れたことは偶然ではない。インドにおける無の実体化はやや度が過ぎていて、ブラフマグプタ(ब्रह्मगुप्त; 597–668 AD)などは、628年の『ブラーフマスプタシッダーンタ』という天文学書の中で、0+0=0, 0-0=0, 0×0=0 といった演算のみならず、0/0=0[4]といった今日の数学が許容しない演算まで行っている。ブラフマグプタは、ゼロ以外の数をゼロで割る演算に答えを見出さなかったが、これに関しては後のインドの数学者が、ゼロだとか無限量だとか様々な案を述べている。
サンスクリット数学の研究者、林隆夫は、インドが、ゼロを表す記号を持っていただけでなく、世界で初めてゼロを数学的演算の対象とするようになった理由として、(1)空位を空位のまま放置できる算盤や算木を使わずに筆算したため、ゼロを含む加、減、乗、平方を行わなければならなかったことと(2)一次方程式と二次方程式の解を形式的に整えようとすると、ゼロを含む除、開平を行わなければならなかったこと[5]を挙げているが、説得力に欠く。インドでも一世紀以降算盤が用いられていたし、筆算は他の地域でも行われていたからだ。もっと粗末な算盤しかなかったバビロニアでは、二次方程式の解の公式が認知されていたにもかかわらず、ゼロが演算の対象になることはなかった。
無の思想はインド以外では中国にもあった。周の時代の思想家、老子は、「道は空っぽの器の様なもので、それだけでは何の役にも立たないように見えるが、それを満たそうとしても満ちる事がないくらいに遠大なものであり、その懐の深さは万物を生み出す根源の深さでもある[6]」と言って、道を、無にして万物を生み出す根源とみなしていた。老子の影響なのか、周の時代から前漢の時代に書かれた『九章算術』には、零を含む演算の規則が書かれている。
引き算においては、同符号なら引き、異符号なら足す。無入から正を引くと負で、無入から負を引くと正である。[7]
この文における「無入」がゼロに相当する。x>0 とすると、引用文の言わんとすることは、0-x=-x, 0-(-x)=x ということなのだが、『九章算術』は、無入に相当する記号を作らず、空白のままにしていた。インドの数学がゼロに相当する記号を考案し、かつそれを数字として扱うようになったのは、インド哲学には、中国哲学以上に無を実体化する傾向があったからと言うことができる。
インド式計算法は、イスラムの数学者で天文学者のアル=フワーリズミー(عَبْدَالله مُحَمَّد بِن مُوسَى اَلْخْوَارِزْمِي; c. 780 – c. 850)が825年に著した『インドの数の計算法』に受け継がれた。この本は12世紀にラテン語に翻訳され、その計算法は、アル=フワーリズミーのラテン語名から、アルゴリズムとして知られるようになった。また、インド起源の数字はアラビア数字としてヨーロッパでも普及することとなった(以下の図を参照)。サンスクリット語で「空」を意味するシューニヤ(śūnya)は、そのアラビア語訳「スィフル(صِفر)」を経て、イタリア語の「ゼフィロ(zefiro)」、英語の「ゼロ(zero)」となった。だが、ゼロが数字として認められるようになったころには、西暦はデ・ファクト・スタンダードとしてヨーロッパで定着してしまっており、今日に至るまで、ゼロの存在しない時間軸が使われている現状に変化はない。

ヨーロッパ人、遡って古代ギリシア人はなぜゼロを拒否したのか。それは、彼らが完全主義だったからだ。ユークリッドの『原論』が典型的に示しているように、ギリシア人は、厳格な論証に基づく整然たる公理システムを築こうとした。インドの数学では9世紀にも存在した確率論が、ヨーロッパでは真空論と同様にパスカルの時代まで存在しなかった[9] のも同じ理由による。確率でしか未来を語れないことは認識能力の欠如を意味しており、ギリシア人はそれを嫌ったのである。ギリシア人は完全主義者であったがゆえに、無、真空、ゼロ、不確定性を認めようとはせず、それらを有で埋めようとしたのだ。その理想は立派なのだが、結果は皮肉なもので、ギリシアの数学は、完全にしようとしたがゆえに、かえって不完全になってしまった。
古代ギリシア、古代ローマ、そして中世ヨーロッパが、位取り記数法(positional notation)、別名、位値記数法(place-value notation)ではなくて、記号値記数法(sign-value notation)を採用していたことも、ゼロに対する嫌悪の結果と考えることができる。位取り記数法は、例えば、十進法の場合、0から9までの有限な個数の数字で無限に多くの数字を表すことができるという点で、そうではない記号値記数法よりも優れている。ところが、古代ギリシア人は、先進的だったバビロニアの位取り記数法ではなくて、後進的なエジプトの記号値記数法に倣った独自のアルファベット記数法を作り上げた。天文学者の中には、バビロニアの六十進法を使う者もいたが、一般には普及しなかった。その結果、ギリシア人は、1未満の数を表す時、小数ではなくて、エジプト式分数を使わざるを得なかった。
エジプト式分数とは、例えば、5/6=1/2+1/3 というように、分数を分子が 1 の分数の和で表す分数の表記法である。以下の図に示すように、エジプトの記数法では、1/N という形の分数は、自然数 N の上に逆数記号を付けることで表すことができた。

ところが、エジプト人は、2/3 のような分数を、私たちが今日やっているように、2 と 3 という既存の数字から作らず、2/3 だけを表す特殊なグリフで表した。2/3 ほどよく使われなかったが、3/4 を表す特殊記号もあった。このような方法で分数の数だけ特殊記号を作っても、全部覚えることはできないので、エジプト人は、分数を分子が 1 の分数の和で表したのである。ヨーロッパ人は、古代ギリシアの時代から中世に至るまでこの不便極まりないエジプト式分数を使っていた。
以上を要するに、ゼロを嫌ったヨーロッパ人は、ゼロを含んだ位取り記数法を拒否し、ローマ数字を使った記号値記数法を用いた。そのため、限られた数しか表現できず、ヨーロッパの算術は、中世まで、離散量である自然数を用いた演算の域を大きく超えない水準にとどまった。このような後進的な記数システムしか持たなかった時代に形成された付番システムに人類がこれからも拘束され続けるのはいかがなものかという問題意識から、離散的な自然数を単位として時間を同定するシステムを連続的な実数からなる時間軸上で時点を同定するシステムに変換する方法を次に考えてみたい。
2. 時間システムを時点システムにする方法
時間を一定の間隔で分割し、各スパンに自然数で番号を割り振っていく時間システムと、時間軸を実数軸とみなして、時点を位置付ける時点システムとの違いを以下の図で説明しよう。
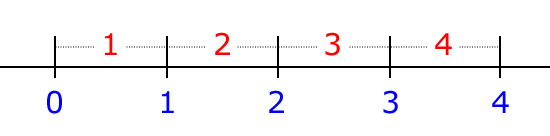
ヨーロッパの紀年法や暦のシステムにおける数字は、この図で赤色に書いた数字に対応する。ゼロは存在せず、各時間間隔に、1, 2, 3 … と自然数の番号が付けられる。各自然数は、自らの長さを1とするので、時間間の間隔を求める時は、差に1を加えなければならない。例えば、2日から4日までの日数は、4-2+1=3 (日)としなければならない。ところが、時点は、この図の青色で書いた数字に対応しており、数直線における点と同様、自らの長さがゼロなので、差にそれを加える必要がない。今、時点 t1=1、時点 t2=4 とすると、時点間の間隔は、4-1=3 となる。
連続量による付番システムは、すべての実数値を時点として扱うことができるという点で離散量による付番システムよりも優れている。他方で、離散量による付番システムは、連続量による付番システムよりも直観的にわかりやすいという長所を持つ。したがって、離散量による付番システムを全面的に否定するべきではないが、離散量による付番システムを連続量による付番システムに対応させる方法を考えなければならない。連続的な時間を非連続な整数値に対応させるには、アイバーソン(Kenneth Eugene Iverson; 17 December 1920 – 19 October 2004)が提案した関数である天井関数と床関数[10]を使えばよい。すなわち、年、月、日は、天井関数で対応させ、時、分、秒は、床関数で対応させればよい。どちらも連続的な時間を非連続な整数の時間に対応させる関数であるが、前者が1から始まるのに対して、後者は0から始まる。
天井関数とは、実数 x に対して x 以上の最小の整数を対応させる関数である。
グラフにすると、以下のようになる。
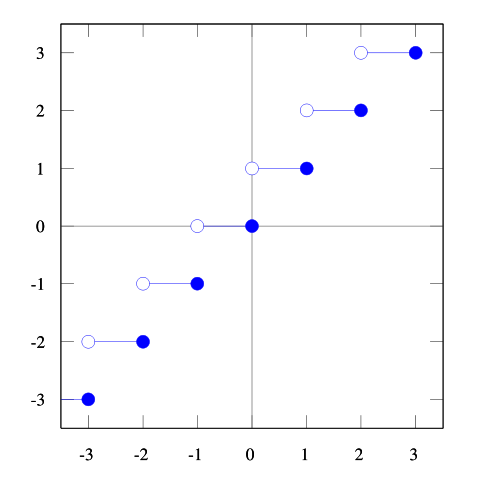
月は、0日ではなくて1日から始まり、年は、0月ではなく、1月から始まり、西暦は、0年ではなくて、1年から始まる。だから、これらは天井関数の値であるということができる。世紀も100年を単位とする天井関数で、例えば、1945年は19世紀ではなくて、20世紀になる。このように一つずれているのは、最初が1世紀で、0世紀ではないからだ。
床関数とは、実数 x に対して x 以下の最大の整数を対応させる関数である。
グラフにすると、以下のようになる。
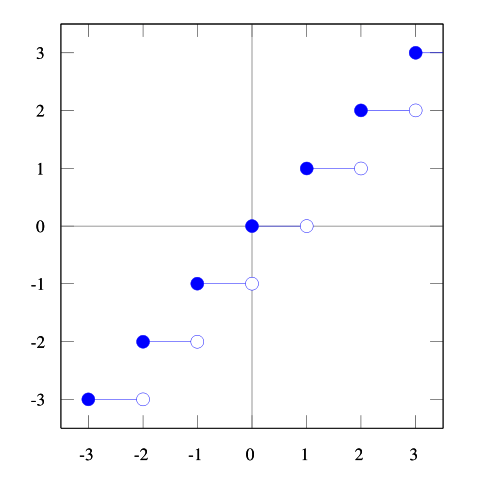
時、分、秒を下位単位とする時刻システムは、伝統的にはゼロベースではない。しかし、24時制の時刻システムは、24:00 を 00:00 とするならば、ゼロベースの付番システムになる。
同じ時間軸上の座標を定めるのに、天井関数と床関数が混在しているのは、不都合である。暦では、新しい年は12月からではなくて1月から始まるというのに、時刻では、午前と午後の切り替えは1時ではなくて12時からである。00時00分を24時00分と表記して前の日の最後の瞬間とみなす人はいるが、00時01分が次の日に属することを否定する人はいない。ところが、西暦では、2000年9月15日から始まったシドニー・オリンピックは、21世紀最初のオリンピックではなくて、20世紀最後のオリンピックである。二つの関数の混在は混乱のもとだからどちらかに統一した方がよい。
では、天井関数と床関数のどちらで統一するべきだろうか。天井関数では、各期間の最後にゼロが来ることになる。実際コンピュータのプログラムでは、1899年12月31日をデフォルトの基準、00年00月00日とすることが多い。しかし、ゼロは期間の最後よりも最初に来た方が本来的である。コンピュータ・プログラムは一般人が直接目にするものではないから、こうした不自然なトリックを使ってもよいのだが、暦は一般人が目にするものだから、直観的にわかりやすくする必要がある。だから、統一するなら床関数で統一した方がよい。次節以降で示すように、下位単位がある時には、床関数で連続的な時点システムを近似した方が、計算が簡単になる。
3. 床関数で時点システムを近似する利点
床関数で時点システムを近似する利点は、時点を変数とする演算が容易になるというところにある。ここでは、演算の簡単な例として、時点間の時間を求める演算をとりあげ、その便利さを示すことにしよう。しかし、その前に、床関数によって丸めた数字を使って時間を求めることで、どのような誤差が生じるのかを考えなければならない。今、時点 t1 と時点 t2 を床関数で丸めた数字を T1 と T2 とする。
すると、T1 と T2 の差には、プラスマイナス1未満の誤差が生じることになる。
なお、天井関数の場合は、以下のようになる。
差を求めると同じになるが、整数値と時点との関係が複雑になるので、床関数の方がわかりやすい。
このことをふまえて、以下の問題を解いてみよう。まずは、もともと床関数である時間の計算から始めたい。
ある月の1日の21時45分から2日の3時15分までの時間を求めよ。但し、1分未満の誤差は無視せよ。
単位を時で統一して計算すると、
5時間30分であることがわかる。
次に天井関数の日の計算をしてみよう。ISO 8601[13] で定められているように、紀元前1年を西暦ゼロ年として、西暦を正負の値を取るゼロベースの付番システムにするなら、以下のような問題も、床関数に変換することで、解くことができる。
紀元前63年9月23日に生まれ、西暦14年8月19日に死亡したアウグストゥス(オクタウィアヌス)が生きた期間を求めよ。但し、1日未満の誤差は無視せよ。
ゼロベースの付番システムでは、紀元前63年は、-62年となる。9月23日はその年の296日目に当たり、8月19日は261日目にあたるが、床関数とみなすなら、それぞれ、295日と260日となる。そこで、単位を年にそろえて、計算すると、
75年と330日であることがわかる。もっとも、9月23日がその年の296日目に当たるとか、8月19日は261日目にあたるといったことは即座にはわからない。この点をもっとわかりやすくするにはどうすればよいかを次に考えてみよう。
4. ゼロベースでゼロベースの暦を作る方法
現在では維持することに合理的理由がなくなった過去の習慣を一切無視して、それこそゼロベースでゼロベースの暦を作るとするならば、どのような時点同定システムが最も合理的だろうか。一日と一年という単位は、地球上に住む私たちの生活サイクルを規定している地球の日周運動と年周運動の周期に基づいており、無視することはできない。しかし、太陰暦においては月齢のサイクルに対応していた月や、月の公転周期の 1/4 に相当する週のサイクルは、太陽暦では意味をなさないので、無視することができる。また、時間が12/24進法で、分と秒は六十進法であるが、古代バビロニア以来のこの伝統も、分割しやすいという以上のメリットがないので、これも現在の主要な記数法である十進法にすることができる。
こうした暦の合理化の試みは過去にあった。過去から続く伝統の呪縛を無視して、全く新しい合理的暦を作ろうとするなら、過去を無視しようとした過去を無視してはいけない。1793年に、フランス革命政府によって作られた革命暦(calendrier révolutionnaire français)ないし共和暦(calendrier républicain français)がそれである。フランス革命暦では、1週は10日、1日は10時間、1時間は100分、1分は100秒とすべて十進法で再定義された。以下の写真は、1日が10時間となるように作られたフランス革命当時の時計である。

中国でも、かつて1日を100刻に分割し[16]、10日を1旬とする十進法的な時間システムが使われたことがあったから、世界初というわけではないが、フランス革命暦は、少なくとも、ヨーロッパでは最初の十進法の時間システムであった。
フランスは、度量衡も合理化しようとして、地球の子午線弧長の1000万分の1の長さを1メートル、1立方デシメートルの水の質量を1キログラムと定義し、十進法に基づく単位のシステムを用いることを1791年に決めた。このメートル・グラム法は、今日世界のほとんどの国で採用されている。もしもフランス政府がこのような提案をしていなかったなら、1ヤード = 3フィート = 36インチ = 1/1760マイル、1ポンド = 16オンス = 7000グレーン = 1/2240トンというイギリスのヤード・ポンド法が今頃世界で使われていることだろう。
10進法のメートル・グラム法に慣れている私たちからすると、ヤード・ポンド法は複雑怪奇で不便であるように見える。実際これらの単位を使って計算しようとすると、複雑な分数式になるので、不便である。しかし私たちが使っている1日=24時間=1440分=1/7週という単位システムもそれに勝るとも劣らず複雑怪奇であり、計算する上で不便である。もしもフランス革命暦が、メートル・グラム法とともに世界中で採用されていたならば、時間の単位は、今よりもずっと合理的になっていただろう。
フランス革命暦は、当時のアイデアとしては極めて合理的であったが、今から見ればまだまだ非合理な要素を残している。まず、本稿の主題であるが、この暦はゼロベースではなかった。革命暦は、グレゴリオ暦で1792年9月22日に相当する日を1年1月1日としており、年月日のいずれもが1から始まっていた。また30日を1月とする慣習を受け継いでいた。もしも1年以下の単位をすべて十進法にしようとするならば、100日を1月とするべきである。もしも、革命暦が、100日を1月とし、月、週、日が 0 から始まるとするならば、1年における任意の時点を10進法の数字として表すことができるし、以下のような演算も簡単に行うことができる。
1日に1000個の割合で製品を作る機械があるとする。この機械を1月9週8日7時65分からコンスタントにフル稼働したとするならば、2月0週0日0時0分には何個の製品を作っていることになるか。但し、1分未満の誤差は無視せよ。
1月9週8日7時65分と2月0週0日0時0分という時点は、日を1とすると、それぞれ、198.765 と 200.000 というようにストレートに表すことができる。そこから先は、(200.000-198.765)×1000=1235(個)というように、通常の算術で計算できる。先ほど行った計算とは異なり、24や60が分母の分数が出てこないので、それだけ計算が楽である。もちろん、1年を365(366)日としているので、年を単位とするならば、365(366)を分母とする分数を使うことになるが、日を単位とする限り、年を越えた計算でも分数は不要である。
5. 世界暦をゼロベースの暦にする方法
フランス革命暦は、あまりにもそれまでの習慣と異なりすぎたため、その合理的性格にもかかわらず、普及することはなかった。デ・ファクト・スタンダードは、いったん定着してしまうと、容易には変更できないものである。月や週といったサイクルは、今日では月齢サイクルとの関連を失っているが、自然的意味を失っても、二次的に派生した文化的、社会的意味は失われていないから、簡単には廃止できない。そこで、改暦をする時には、過去から受け継いだ習慣をできるだけ尊重し、不具合だけを改めるべきだということになる。
1930年10月21日にエリザベス・アケイリス(Elisabeth Achelis; 1880 – 1973)が世界暦協会(The World Calendar Association)を設立し、提案した世界暦はその代表である。世界暦とは、毎年、日と曜日を固定させる固定暦の一つで、アケイリスが提案した世界暦は以下のようなものであった。

このカレンダーを見ればわかるように、世界暦を構成する四つの四半期(1-3月, 4-6月, 7-9月, 10-12月)は、どれもが日曜日から始まり、13週×7日/週=91日、3か月(それぞれ、31, 30, 30 日)から成り立っている。但し、それだけは1年が364日となってしまうので、公転周期とのずれをなくすために、世界暦には二種類の無曜日が挿入される。一つは年末に毎年挿入される「世界日」で、もう一つは閏年に第二四半期末に挿入される「閏年日」である。これらの無曜日は、週のサイクルの外部に位置し、世界的に休日として扱われる。
世界暦には以下のようなメリットがある。
- 日と曜日の関係が固定されているので、毎年新しいカレンダーを作る必要はないし、それどころか一年分のカレンダーを作る必要すらない。四半期分のカレンダーのテンプレートを作っておけば、それを繰り返し使うことができる。
- 世界暦では、恒例行事の実施時期を年単位または四半期単位の特定の日と曜日に固定することができるので、覚えやすい。現在のように、行事の実施時期や曜日を休日や祭日との関係で毎年変更しなければならないのは不便である。
- 現在の四半期は、90日、91日、92日、92日と不揃えで、最大2日の差があるが、世界暦では各四半期はすべて91日で、無曜日を前月に繰り入れても、差は1日だけなので、四半期ごとに行われる決算を正確に比較することができる。
- 現在の月の日数には最大で3日の差があるが、世界暦では無曜日を入れても差は1日だけなので、月単位の統計値もより正確に比較できる。日曜日を除いた平日は、毎月26日で一定であり、月給は同じ労働時間に対して支払われる[17]。
アケイリスの世界暦もまたゼロベースではなかった。そこで、これをゼロベースの暦にしてみよう。以下の表にあるように、各四半期の日をゼロから始まる通番にし、月や週の番号もゼロから始まるようにしてみよう。通番にすることで、数字がやや大きくなるが、すべて2桁以下であり、それほど煩わしくはない。
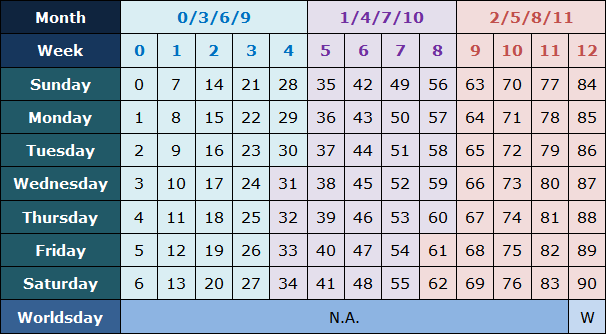
私が提案するこの世界暦には、以下のようなメリットが新たに加わる。
- 各日を7で割ることで、何週目の何曜日かがわかる。例えば、73日は、7で割ると商が10で余りが3であることから、第10週第3曜日(水曜日)であることがすぐにわかる。これに対して、現在の暦ではユリウス通日に換算してから7で割らないと曜日がわからない。
- 日、曜日、週、月すべてをゼロベースにすることで、どの単位を使って時点を表しても、それを時間軸上の座標として近似することができるようになる。その結果、時点を変数とする演算が容易になる(簡単な例を後で挙げる)。
- アケイリスの世界暦には、キリスト教徒が不吉と信じている13日の金曜日が1年に4回も存在するが、ゼロベースの通番にすると、一日ずれるので、それが皆無になる。13日自体は相変わらず存在するが、13番目の週はなくなる。
- 月末の最終日が、30日、60日、90日というように、30の倍数となり、覚えやすい。月末の最終日は、様々な契約の期限として指定されることが多いのだが、現行の暦だとそれが何日であるか覚えにくいし、間違いやすい。
日を通番にすることで、月という単位がなくなることはないにせよ、月の独立性が低くなり、代わって、四半期の重要性が増す。だから、第0曜日に「日曜日」、第1曜日に「月曜日」というように親しみやすい名前を付けたように、四つの四半期にも親しみやすい名前を付けるべきである。そして、一年を四つに分割するなら、それを最もポピュラーな四分割である四季に対応させるとよい。四季を分節する季節は天文学的には、冬至、春分、夏至、秋分である。冬至と夏至は、太陽の南中高度が最低または最高になる時点であるが、気温に基づく冬と夏のピークはその極値から1か月余り遅行するので、北半球であれ、南半球であれ、冬季と夏季は、冬至または夏至から春分または秋分までとするのが適切である。
一年の始まりをいつとするかは、太陽暦を採用した地域によっても異なっていた。最古の太陽暦である古代エジプト暦では、一年の始まりは、もともとはナイル川の洪水が始まる7月の中旬ごろであった。エチオピア暦では、9月7日から新年が始まる。太陰太陽暦であるバビロニア暦は、春分の頃の新月の直後を元日としており、ユダヤ暦、グレゴリオ暦の最古の起源であるロムルス暦、イラン暦、ヒンズー暦は、いずれも春分の頃を一年の始めとしている。古代の中国では、年始は冬至頃に設定されたが、前漢の時代以降、冬至と春分の中間に位置する立春の頃を年初とするようになった。マヤのハアブ暦も、もともとは冬至を年初としていた。
このように、暦をいつから始めるかは、文化によって様々であるが、現行のグレゴリオ暦からの変更を最小にするには、冬至から始めるべきである。冬至は例年12月21日あるいは22日であることが多いので、12月21日を世界日とし、12月22日を0月0日としよう。すると、ゼロベースの世界暦とグレゴリオ暦との対応は以下のようになる。
| 四半期名 | 世界暦での月日 | グレゴリオ暦での月日 |
|---|---|---|
| 冬季(第0四半期) | 0月0日~2月90日 | 12月22日~3月22日 |
| 春季(第1四半期) | 3月0日~5月90日 | 3月23日~8月21日 |
| 夏季(第2四半期) | 6月0日~8月90日 | 6月22日~9月20日 |
| 秋季(第3四半期) | 9月0日~11月90日 | 9月21日~12月20日 |
これをみるとわかるように、冬至の日を0月0日に選んだからといって、春分(3月20-21日)、夏至(6月20-21日)、秋分(9月22-23日)が各四半期の0日になることはない。なぜなら、地球の公転軌道は楕円であり、ケプラーの第二法則により、遠日点を通過する春分から夏至を経て秋分に至る期間は、近日点を通過する秋分から冬至を経て春分に至る期間よりも数日長くなるからだ。だが、季節の四分点は、ほぼ各四半期の境界付近にあり、私たちの季節の感覚と大きくずれていないので、これでよいだろう。
次に、月番号に月名を付けよう。グレゴリオ暦では、1月から12月までの月に英語で以下のような固有名詞が割り当てられている。
- 1月: January
- 2月: February
- 3月: March
- 4月: April
- 5月: May
- 6月: June
- 7月: July
- 8月: August
- 9月: September
- 10月: October
- 11月: November
- 12月: December
ところが、ローマ暦の最古の暦であるロムルス暦では、1月から10月までしかなく、名称も二つずつずれていた。
- 1月: Martius (マルティウス、31日)
- 2月: Aprīlis (アプリーリス、30日)
- 3月: Māius (マーイウス、31日)
- 4月: Jūnius (ユーニウス、30日)
- 5月: Quīntīlis (クィーンティーリス、31日)
- 6月: Sextīlis (セクスティーリス、30日)
- 7月: September (セプテンベル、30日)
- 8月: Octōber (オクトーベル、31日)
- 9月: November (ノウェンベル、30日)
- 10月: December (デケンベル、30日)
マルティウスは、春分を含む月で、戦いの神、マルスに由来する。アプリーリスは、ギリシアの美の女神、アフロディテ(ビーナス)に由来する。マーイウスは、ギリシアの神マイアではなくて、ローマ固有の古い神で、豊饒を司る農耕神である[18]。ユーニウスは、ユノーすなわち、ギリシアの女神ヘラで、女性の守護神である。それ以降はラテン語の序数詞から命名されている。10月は冬至の頃に終わり、そこから春分までは農作業がなかったので、暦もなかった。しかし、それでは不便なので、ロムルスを継いだヌマ王(Numa Pompilius; 753–673 BC; reigned 715–673 BC)が、二つの月を付け加えた。
- 11月: Ianuarius(ヤーヌアーリウス、29日間)
- 12月: Februārius(フェブルアーリウス、28日間)
その後この二つの月が1月と2月になり、クィーンティーリスは、ユリウス・カエサルの名に因んでユリウス(Julius)、セクスティーリスは、ローマ皇帝アウグストゥスの名に因んでアウグストゥス(Augustus)に変更され、今日に至っている。
以上の成立経過を踏まえるならば、ゼロベースの世界暦に月の固有名を適用するにあたって、以下のように、1月から10月までをロムルス暦の本来の番号に対応させることを考えてみたい。
- 0月: February
- 1月: March
- 2月: April
- 3月: May
- 4月: June
- 5月: July
- 6月: August
- 7月: September
- 8月: October
- 9月: November
- 10月: December
- 11月: January
“January”は、ヤヌス(Janus)に由来する。ヤヌスは、前後に向いた二つの顔を持ち、過去と未来に視線を向ける神であるから、“January”は、年初の月名にふさわしいと同時に、年末の月名にもふさわしい。“February”は、フェブルウス(Februus)に由来する。フェブルウスは、慰霊祭フェブルアーリア(Februaria)の主神で、この慰霊祭では、再生の月であるマルティウスに先立って、フェブルウスが死者の魂を慰霊し、清める神で、冬至の後の月の名としてふさわしい。以上は、英語の月名であるが、日本語の場合、0月は師走、1月は睦月というように、旧暦で使っていた別名を使えばよい。
名称の話はこれで終わりにしよう。ゼロベースの世界暦は、ゼロベースのフランス革命暦と比べれば、グレゴリオ暦と妥協した暦であるが、ゼロベースである以上、その日付を座標として扱った演算をすることができる。また一問解いてみよう。
2050年秋季第4週火曜日から2051年春季第10週金曜日まで何日あるか。但し、1日未満の誤差は無視せよ。
秋季は第3四半期、第4週火曜日は、4×7+2=30日、春季は第1四半期、第10週金曜日は、10×7+5=75日であるから、2051×365+91×1+75-(2050×365+91×3+30)=365-91×2+45=228(日)となる。時、分、秒といった下位の単位を用いる場合も同様に計算できる。
こうした合理性にもかかわらず、世界暦に反対する人たちは、無曜日の挿入によって週が不連続になることを問題視している。年末年始はどのみち特別スケジュールになるので、無曜日が一日挿入されたからといって特に混乱することはないが、ユダヤ教、キリスト教、イスラム教といったアブラハムの宗教の信者は、六日間働いた後の七日目の日を安息日とすることを神との契約で決めており、無曜日を休日として挿入することは神との契約に反するという理由で反対している。たしかに、旧約聖書の『出エジプト記』には、以下のように、モーセの十戒の四番目の戒律として、安息日に休むことが挙げられている。
安息日を覚えて、これを聖とせよ。六日のあいだ働いてあなたのすべてのわざをせよ。七日目はあなたの神、主の安息であるから、なんのわざをもしてはならない。あなたもあなたのむすこ、娘、しもべ、はしため、家畜、またあなたの門のうちにいる他国の人もそうである。主は六日のうちに、天と地と海と、その中のすべてのものを造って、七日目に休まれたからである。それで主は安息日を祝福して聖とされた。[19]
これを読めば分かるように、神は、六日間働いた後の七日目を休めと命じている。しかし八日目に働いてはいけないとはどこにも書いていないし、七日間を一週間として同じことを繰り返せとも書いていない。そもそも、この戒律の根拠となっている『創世記』には、神は天地創造の七日目に休んだ[20]とあるが、八日目に何をしたか、あるいは天地創造の以前に何をしていたかについては何も書かれていない。もしも神が八日目に天地を破壊し、しかる後に世界を再創造し、十四日目に完成させて休むというように、七日ごとに同じことを繰り返すなら、七日目ごとに休むという現在の習慣は正当化されるが、聖書にはそのような記述はない。ゆえに、安息日の翌日を休んだからといって、第四の戒律に反することにはならない。
安息日(英語:Sabbath;ヘブライ語:שַׁבָּת)は、「中間的な休み」を意味するバビロニア語の“sabattum”、あるいはシュメール語の“sa-bat”に由来する。古代メソポタミアでは、新月から数えて、7日目ごとを祝っていたが、安息日は28番目の日にあり、週単位ではなくて、月単位にあった。といっても月の周期は、29-30日なので、最初の三つの週は7日でよいとしても、最後の週は、8-9日にしなければならなかった。聖書が7日単位の週の厳格な反復にまで触れていないのは、こうしたバビロニアでの習慣の影響と考えられる。
アブラハムの宗教の信者は世界に多数いるが、実際に安息日にこだわっているのは、人口という点では少ないユダヤ教徒と一部のキリスト教徒だけである。イエス・キリストは自ら安息日の戒律を破り、それを非難したパリサイ人に対して、「人の子は安息日の主である[21]」と述べたと『ルカ福音書』は伝えている。つまり、人間のために安息日があるのであって、安息日のために人間があるのではないということである。
そもそも、七番目の日である土曜日を安息日として休日にしているのは、ユダヤ教徒とセブンスデー・アドベンチスト教会(The Seventh-day Adventist Church)のキリスト教徒だけである。それ以外のキリスト教徒が日曜日を休日としているのは、キリスト教を公認したローマ皇帝コンスタンティヌス1世が、321年に古代ペルシアにおける太陽崇拝の宗教であるミトラス信仰を取り入れ、太陽の日である日曜日をキリスト復活の日として休日にしたこと[22]が起源であり、日曜日を休日とすることは本来のキリスト教の教義ではない。休日を土曜日にしようが、日曜日にしようが、どちらにしても、無曜日をはさんで休日が二回続くことになるが、これまで述べた理由により、宗教的伝統の否定につながるとは言えない。イスラム教では金曜日を集団礼拝(サラート=ル=ジュマァ)の日としているが、イスラム教はグレゴリオ暦とは異なる独自の太陰暦にしたがって休日を決めているので、グレゴリオ暦を改変しても影響を受けない。
以上、私が最も合理的で理想的と考えるゼロベースの世界暦の案を披歴した。もちろん、暦は、合理的だからといって普及するわけではない。それは、人工言語のエスペラント語が合理的だからといって英語に取って代わって国際補助語として使われるわけではないのと同じことである。デ・ファクト・スタンダードは、いったん確立してしまえば、容易に変更することはできないのである。変更が可能かどうかという議論は措くとして、仮にグレゴリオ暦からこの暦に移行するとするなら、いつがよいだろうか。実は、2013年の冬至の日である12月22日は日曜日である。この日を2014年0月0日とすれば、ゼロベースの世界暦にシームレスに移行することができる。移行するべきかどうかは、読者の皆さんの判断に委ねよう。
6. 参照情報
- ↑実は、ヨーロッパでは、0どころか1までもが数字として扱われていなかった。1は単位であり、数字は、単位から作られる複数に限定されていたのである。1を初めて数字として扱ったのは、シモン・ステヴィン(Simon Stevin; 1548 – 1620)の1585年の著作『算術(L’Arithmétique)』である。
- ↑Αριστοτέλης. Φυσικής Ακροάσεως.Βιβλίο 4, Κεφάλαιο 6-9.
- ↑“Ἀριστόξενος δ’ ἐν τοῖς Ἱστορικοῖς ὑπομνήμασί φησι Πλάτωνα θελῆσαι συμφλέξαι τὰ Δημοκρίτου συγγράμματα, ὁπόσα ἐδυνήθη συναγαγεῖν, Ἀμύκλαν δὲ καὶ Κλεινίαν τοὺς Πυθαγορικοὺς κωλῦσαι αὐτόν, ὡς οὐδὲν ὄφελος. παρὰ πολλοῖς γὰρ εἶναι ἤδη τὰ βιβλία." Διογένης Λαέρτιος. Βίοι καὶ γνῶμαι τῶν ἐν φιλοσοφίᾳ εὐδοκιμησάντωνΒιβλίον Θ’, 40.
- ↑Brahmagupta. Brahmasphotasiddhaantasya. Nāga Pabliśarsa; 1. saṃskaraṇa edition (1999). §. 18.34.
- ↑林隆夫. 『インドの数学―ゼロの発明』中央公論社 (October 1, 1993). p. 41-43.
- ↑“道沖而用之 有弗盈也 潚呵 始萬物之宗" 老子. 『道德經』帛書校勘版. 第四十八章.
- ↑“正負術曰:同名相除,異名相益,正無入負之,負無入正之" 『九章算術』8. 方程, 3.4. 中國哲學書電子化計劃.
- ↑RTPking. “Numbers in languages like, Sanskrit, Telugu, English and Urdu“. 5 December 2012. Licensed under CC-BY-SA.
- ↑Ian Hacking. The Emergence of Probability. Cambridge University Press (August 31, 1984). p. 8.
- ↑Kenneth E. Iverson. A Programming Language. John Wiley & Sons (January 1962). p. 12.
- ↑Omegatron. “Graph of the ceiling function." 11 April 2006. Licensed under CC-BY-SA.
- ↑Omegatron. “Graph of the floor function." 30 March 2006. Licensed under CC-BY-SA.
- ↑The International Organization for Standardization. “ISO 8601:2004(E)." 4.1.3.3. Third edition 2004-12-01.
- ↑Cormullion. “A clock made in Revolutionary France, showing the 10-hour decimal clock“. Licensed under CC-BY-SA.
- ↑Rama. “Clock dial of the French Revolution." Licensed under CC-0.
- ↑Joseph Needham, Ling Wang, Derek J. De Solla Price. Heavenly Clockwork: The Great Astronomical Clocks of Medieval China. Cambridge University Press; 2 edition (November 28, 1986). p. 199.
- ↑アケイリスが生きていた時代には週休二日ではなかったので、土曜日は休日としてカウントされていない。また祭日を各月に不均等に入れれば、各月の労働時間はそれだけ均等ではなくなる。
- ↑岡田 芳朗, 後藤 晶男, 伊東 和彦, 松井 吉昭. 『暦を知る事典』東京堂出版 (May 1, 2006). p. 28-29.
- ↑“זכור את־יום השבת לקדשו ׃ ששת ימים תעבד ועשית כל־מלאכתך ׃ ויום השביעי שבת ׀ ליהוה אלהיך לא־תעשה כל־מלאכה אתה ׀ובנך־ובתך עבדך ואמתך ובהמתך וגרך אשר בשעריך ׃ כי ששת־ימים עשה יהוה את־השמים ואת־הארץ את־הים ואת־כל־אשר־בם וינח ביום השביעי על־כן ברך יהוה את־יום השבת ויקדשהו׃ ס" The Old Testament.Exodus. Chapter. 20. Verse. 8-11.
- ↑The Old Testament.Genesis. Chapter. 2. Verse. 2.
- ↑“κύριος ἐστιν τοῦ σαββάτου ὁ υἱὸς τοῦ ἀνθρώπου." The New Testament.Luke. Chapter. 6. Verse. 5.
- ↑Eviatar Zerubavel. The Seven Day Circle: The History and Meaning of the Week. University of Chicago Press; Reprint edition (March 15, 1989). p. 45.





















ディスカッション
コメント一覧
まだ、コメントがありません